基本構造と動作
これからコンピュータの構造と動きを段階を経て理解していきます。と言っても直接コンピュータの動きではイメージしにくいので、理解しやすいように別のもので考えていきます。
銀行や郵便局の窓口をイメージして下さい。窓口の中、つまりお客さん対応をする方にあなたがいると思ってください。窓口の中には机があり、机の上には、「手順書」「ホワイトボード」「電卓」が置いてあります。窓口には「足し算係」と札がかけてあり、この窓口では、お客さんから言われた数を足して答えを教えるサービスを行っています。まあ、あり得ない窓口ですが、そこは我慢してイメージしてください。このサービスのために、あなたがやることは、手もとの「手順書」に書かれている手順通りに行動することです。
では、この「手順書」の中身を見てみましょう。
| 言われた数をホワイトボードに記入する |
| 次に言われた数をホワイトボードの別の場所に記入する |
| ホワイトボードに書かれた数を電卓で足し算する |
| 足し算の結果をホワイトボードに記入する |
| ホワイトボードの数を報告する |
一番最初の手順を見ると、「言われた数をホワイトボードに記入する」とあります。あなたはその通りに、お客さんから聞いた数をホワイトボードに書きます。手順書の次に進むと、「次に言われた数をホワイトボードの別の場所に記入する」とあります。そこで同様に、次の数を聞いてその数をホワイトボードに書きます。手順書の次には、「ホワイトボードに書かれた数を電卓で足し算する」と書いてありますので、二つの数を電卓に入れて足し算を行います。手順書の次を見ると、「足し算の結果をホワイトボードに記入する」とあります。そこで転記します。手順書の次は、「ホワイトボードの数を報告する」とあります。そこであなたはお客さんにその数を伝えます。これで、あなたは「足し算係」としての仕事をこなしたことになります。
以上がコンピュータを理解していただくために例えた「足し算係」の説明は終わりです。いかがですか? 簡単ですね。「いやいや、コンピュータがこんな単純なはずがない」と思われるかもしれませんが、まさにこのままの動きなのです。とりあえず、このイメージを明確に持ってください。その上で、きちんとした理解のために、少しづつ深堀していきたいと思います。
まず、この「手順書」をコンピュータでは、「プログラム」と呼びます。上記の動作で、あなたが「足し算係」として動いたのは、この手順書に「足し算係」として動く手順が記載されていたからです。もし、3番目の手順に「・・引き算する」と書かれていたら、あなたは「引き算係」として動いたわけです。このように「プログラム」は、コンピュータの動作を決定する重要な役割を担っていることを理解してください。逆に言えばあなたの意思はなく、何も考えることなく手順書に従うのみで、意味ある仕事として完結できるのです。
次に、このプログラムは、幾つかの手順に分かれて記載されていたことに注目してください。これは、コンピュータが一回に実行できる処理に依存します。この一回に実行できる処理を「命令」と呼びます。この「命令」は、本当に単純なことに限られています。上記の例では、「数をホワイトボードに書く」とか「ホワイトボードの値を電卓に入れて計算する」といったことです。つまり、「二つの数を受け取って加算した結果を報告せよ」と書いてなくて、細かい処理に分かれていたのには理由があったわけです。また、この命令として書ける内容は「電卓」の機能にも依存します。例えば、「電卓」が加算と減算しかできないものだったとした場合、命令として「掛け算をする」とは書けません。もし、この加減算のみの電卓で、「掛け算係り」をやらせたいのであれば、最初の数を、次に得た数の分だけ加算するようなプログラムにする必要があります。
次は「ホワイトボード」です。上記では、少し適当に説明してしまいました。実際のコンピュータの内部を意識すると、このホワイトボードには、幾つかの枠があり、それぞれの枠に名前がついています。例えばA欄、B欄、C欄・・・といった形です。ですから、上記の例の最初の命令は、「言われた数をホワイトボードのA欄に記入」になりますし、次の命令は、「言われた数をホワイトボードのB欄に記入」になります。この幾つかの枠に分かれたホワイトボードをコンピュータでは「レジスタ」と呼びます。
最後の「電卓」ですが、コンピュータ用語では、「ALU(Arithmetic Logic Unit)」と呼びます。まあ、わかりにくいので、単純に「演算器」と云うこともあります。このALUは特定のレジスタにつながっていて、このレジスタに値を入れ、ALUを加算実行状態にすると、その加算結果が別のレジスタにでてきます。この演算器に入れる側のレジスタが、CとDで、結果が出てくるレジスタがEだった場合、上記の「ホワイトボードに書かれた数を電卓で足し算する」は正確には以下の命令に分けて記載しなければならないことになります。
(最初に二つの数は、レジスタAとレジスタBに入っている状態です)
| レジスタAの数をレジスタCに転記 |
| レジスタBの数をレジスタDに転記 |
| 加算を実行(この時点でレジスタEに数が出てくる) |
コンピュータとしての動作を明確化してきましたが、ここまでで、まだ、ぼんやりしているのは、処理を依頼している「お客さん」です。これは「コンピュータを利用する人」になるわけですが、お客さんと数のやりとりをする窓口は、コンピュータの用語としては、「入出力装置」になります。この詳細は後ほど説明します。
これまで説明してきた内容は、主に、コンピュータの中でも特に「CPU」と呼ばれる部品の動作になります。とりあえず。ここで重要なポイントをまとめてみます。
- プログラムに従って、命令を順番に実行する
- 命令はCPUが実行できる処理
- CPUには値を保持するためのレジスタがある
上記のポイントを把握した上で、今一度最初から一読いただければと思います。
メモリ
机にある「手順書」「ホワイトボード」「電卓」を使って処理を進めることがコンピュータの動きだったわけですが、ここにもう一つ構成要素を追加します。それは「棚」です。たくさんの枠に区分された棚が手の届くところにあるとイメージしてください。実は「手順書」はこの棚に置いてあります。枠の一つには「命令」、つまり、一回で実行できる処理の指示が入っており、また、枠には番号がついています。このため、「手順書を順番に実行する」ということは、「棚から枠の番号順に命令を取出して実行する」ということになります。言い換えれば、「プログラムは、棚の、ある範囲に順番に格納されている」ということになります。
一方、この棚は「数」の保管場所としても利用されます。数の保持としては、ホワイトボードである「レジスタ」の役割だったわけですが、レジスタは個数が少なく、もっぱら「手元に一時的に持っておいて処理(計算)する」ために使用され、「数」の実際の保管場所としては、この「棚」を利用します。
そろそろ、レジスタや棚に保管される「数」もコンピュータ用語でいきましょう。コンピュータ用語では、「データ」と呼びます。
足し算マシンでは、数少ないデータしか使わなかったわけですが、実際のコンピュータの処理は大量のデータを扱いますので、棚はたくさんの枠を持つ巨大なものが利用されています。この「棚」はコンピュータでは「メモリ」と呼んでいます。また、メモリの枠につけられた番号を「アドレス」と呼びます。
さて、これまで単に「手順書を順番に実行する」と表現してきましたが、上記を踏まえて実際のコンピュータの処理に近づけて表現してみましょう。机の上には「手順書」は無く、手順書の場所(アドレス)を示す特別なレジスタがあります。このレジスタは専ら「次に実行する命令が保管されているメモリのアドレス」を示すためだけに使われ、データの保持を目的とする他のレジスタとは違っています。このレジスタを「プログラムカウンタ」と呼びます。
机についているあなたは、この「プログラムカウンタ」が示すアドレスから命令を取出して実行します。また、命令を一つ取り出すとプログラムカウンタは自動的に次の命令のアドレスを指すように更新されます。これが「手順書を順番に実行する」の正体です。
入出力装置
これまで説明してきました中で、「入出力装置」、つまりコンピュータの外部の人とデータを受け渡しする部分については詳細が出てきてないわけですが、この実体は「棚の中で、裏に穴が空いている枠」になります。今回の足し算マシンでは足したい二つの値を外部の人がコンピュータに渡し、また足し算の結果を報告しますが、これを行うのがこの「穴の空いた枠」です。棚(メモリ)の特定のアドレスには外部とつながっている枠があり、この枠を介して外部の依頼者とデータのやり取りを行います。
コンピュータの入出力装置はたくさんあります。ディスプレイ、キーボードを初めとし、プリンタ、ネットワーク、スピーカー等多種多様です。これらが全て「穴の空いた枠」でつながっていますので、その数も膨大です。例えば、ディスプレイに至っては、画面の点の一つ一つが一つの枠に対応していたりします。本書ではその詳細までは説明しませんが、つながっているイメージだけは持っておいてください。
ここまでで、コンピュータの動作を理解する登場人物(構成)が出そろいましたので、値を2倍する処理を例にプログラムの詳細とその動作を説明します。
まず、棚に格納されているプログラムは以下の通りです。
| アドレス | 命令 |
| #100 | #1000に「0」を格納 |
| #101 | #1000の値をAレジスタに格納 |
| #102 | Aレジスタが「0」であればプログラムカウンタから「2」を引く |
| #103 | Aレジスタの値をCレジスタに格納 |
| #104 | Aレジスタの値をDレジスタに格納 |
| #105 | ALUで加算を実行 |
| #106 | Eレジスタの値を#1001に格納 |
| #107 | プログラムカウンタから「8」を引く |
まず、前提として、アドレス#1000、1001の枠は入出力部で外部とつながっており、#1000が入力(コンピュータに取り込む)用で#1001が出力用とします。また、利用者が「0」を入力してくることは無いものとします。また、スタートの時点でプログラムカウンタは#100となっています。
最初に実行することは利用者から値を受け取ってレジスタに格納することですが、このプログラムでは、#100~#102でそれを行っています。#100はいったんおいておきまして・・・。#101で値をAレジスタに取り出していますが、このタイミングで利用者がセットした値が#1000に入っているかどうかわかりません。コンピュータの実行速度は極めて速いので、必然的に、利用者の入力を「待つ」必要があります。これを考慮し、次の#102の処理を入れてあります。つまり、取り出した値が「0」であれば、未だ利用者からの入力がされていないものとし、プログラムカウンタから「2」を引くことで、取出しの処理に戻ります。プログラムカウンタは命令を取り出すと自動的に次の命令のアドレスを指しますので、「#103」になっているものを、2を引くことで「#101」になり、取出し処理の位置にしているのです。つまり、利用者によって値がセットされるまで、「取出し(#101)」→「確認(#102)」→「取出し(#101)」→「確認(#102)」・・・ を延々と繰り返しているわけです。この処理を確実にするために、#100の「#1000を「0」にする」動作があります。この処理が無いと#1000に何らかの値があるとそれを2倍して結果を出してしまいます。
ここで利用者が値をセットするとプログラムカウンタは変更されませんので、#103の処理を実行することになります。#103~#105の処理で2倍された答が#1001にセットされ、利用者が受け取ることになります。その次の#107の処理は、無条件でプログラムカウンタの値を更新しています。この処理によってこのプログラム全体が繰り返されることになりますが、もし、この処理が無いと#108の枠から命令を取出して実行、次に#109の命令と実行を続けてしまいます。これらの枠には「命令」を格納していないのですが、コンピュータ(CPU)は、この「命令の取出し」「命令の実行」という決められた処理を延々と実行するので、わけのわからない動作となってしまいます。このような動作を「暴走」と呼んでいます。
以上でコンピュータ内の構成要素が概ね出揃いましたので、各種の文献で出てくるコンピュータの内部構造の絵を示します。
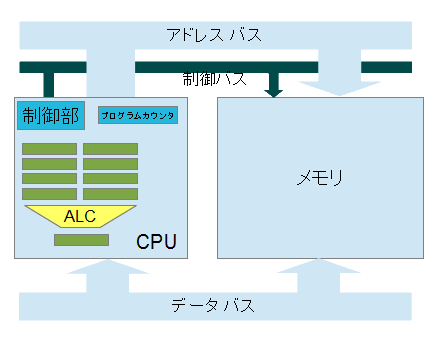
棚とCPUの情報(値やプログラム)のやり取りは、このアドレスバスとデータバスを使って行います。
棚からCPUに情報を取り出す場合は、CPUがアドレスバスに、その取り出す情報が格納されているアドレス値を設定します。すると、データバスにそのアドレスに格納されている値が現れますので、それをCPUが取込みます。 逆にCPUから棚に情報を格納する場合は、CPUがアドレスバスに情報を格納するアドレス値を出した上で、CPUがデータバスに格納する値を出します。すると棚の該当アドレスにその情報が格納されます。CPUから見て取出し動作か格納動作かは、制御バスで指定します。
CPUは、命令を取り出す処理と命令を実行する処理を繰り返して処理を進めていきましたが、命令を取り出す処理では、アドレスバスにプログラムカウンタの値を出し、データバスから命令を取出します。命令を実行する処理で、その命令がメモリから値を取出すものであった場合は、アドレスバスにその取出す先のアドレスを設定します。CPU内の幾つかのレジスタには、このアドレスバスにつなぐことができるものがありますので、そのレジスタを利用することもできます。具体的に「#1000の枠から値を取り出してAレジスタに保存せよ」という命令は、以下のように記述することもできます。
| Dレジスタに1000を格納 |
| Dレジスタに格納されている値が示すアドレスからAレジスタにデータを取出す |
ここで演算器(ALU)について補足しておきます。ALUが実行できる演算は、基本的には、「加算」と「論理演算」と「シフト演算」になります。「論理演算」と「シフト演算」は後で説明します。とにかく、極めて基本的な計算処理しかできません。引き算でさえ、「加算」を利用して行います。これも後述します。
データ
データは、「ビット」と呼ばれる2値情報で表わされます。2値情報とは、情報の最小単位を2つの値で表し、この最小単位を組み合わせて情報を示すものです。私達が普段使っている「数」は、10値情報ですね。10値情報では、一桁という最小単位を0~9の10個の数字で表し、これらを組み合わせて多数の桁で多くの「数」を示します。コンピュータのデータでは、この概念を利用しつつ、最小単位を、便宜上、「0」と「1」の二つで示して利用します。
コンピュータは電気回路として実現されますが、電気回路では、この2値情報だといろいろと便利なことがあります。
電気回路で実現されるコンピュータでは、メモリからCPUへとデータを渡す際、電気(電圧)で状態を伝えるわけで、仮に0V付近を「0」、1.5V付近を「1」としましょう。まあ、この例では、乾電池がつながっていると「1」、つながっていないと「0」と考えていただければいいです。電池が減ってきて1.1Vぐらいになっても、受け側では、「あ、"1"なのね」ということになるでしょう。でも、10値情報だと、1.5Vを10分割して情報を伝えるので、電圧の微妙な変化が値の変化につながってしまいます。つまり間違った情報を伝えてしまうことになります。
また、メモリやレジスタには、「記憶(保持)」という役割があるわけですが、この記憶を電子回路で実現するにも2値情報は適しています。そんなわけでこの「0」と「1」の組み合わせによってデータを表します。
コンピュータは、「計算」を主な役割としていますので、この「0」、「1」の2値情報を、私達が使っている数に対応させて計算します。そこで出てくるのが二進数です。私達が普段使っている十進数と二進数の関係は以下のようになります。
| 十進 | 二進 |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
さて、先に人で模したCPUでお話しました構造ですが、CPUは、棚イメージのメモリからデータを取り出し、レジスタに格納しという処理を行っていました。この時疑問となるのは、棚、つまりメモリのひとつの枠にはいったいどれほどの大きさ(桁)のデータが入るか ということでしょう。つまり、2値情報は「0」「1」の二通り、この最小単位を「ビット」と呼びますが、メモリの一つの枠には、何ビット保持できか ということです。
これはコンピュータによって異なりますが、一般的に利用されている(恐らく皆さんがご利用のPC)では8ビット(1バイト)です(一般にバイトマシンと呼ばれます)。
一方、CPU内のレジスタはどの程度の大きさかというと、これは完全に様々で、昔(初期)のコンピュータは8ビットでしたが、最近のコンピュータは、32ビットのものや64ビットのものが一般的です。これはそれぞれ「32ビットCPU」、「64ビットCPU」と呼びます。
32ビットCPUでは、レジスタのサイズに合わせてデータバスもアドレスバスも32ビットになります(アドレスバスは拡張機能によって変わります。これは後々出てきます)。さて、このように説明しますと「メモリの枠をアドレスで指定するんだよね? その一つの枠の8ビットのデータがデータバスに出てくるんだよね? データバスが32ビットっておかしいじゃん!」となると思います。その通りです。実はこの場合(バイトマシンで32ビットCPU)、一度のメモリアクセスで最大で4枠分のデータが転送されるのです。取出したいのが1バイトデータの場合は、そのデータが格納されているアドレスをアドレスバスで指定しますが、そのデータよりも上のアドレスにある最大で3つの枠分も一気に取り出して、取り出したレジスタでは下位の8ビットのみを利用することになります。「最大で」といちいちことわっているのは、メモリに「ワード境界」というものがあるためです。模式図は以下の通りです。
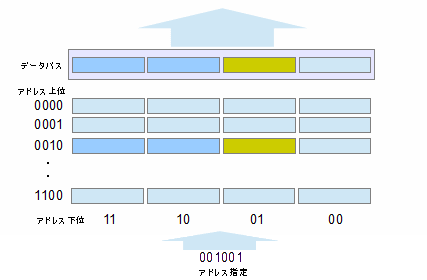
メモリは4つの枠が並んで構成されているイメージで、このワンセットがデータバスにつながります。このため、アドレスが4の倍数の場合は、そのアドレスから上位の4つ分が一気に取り出されます。しかし、4の倍数+1の場合は、そのアドレスから上位3バイトのみが取り出せ、4の倍数+3の場合は、1バイトしか取り出せません。この境界を「ワード境界」と呼んでいます。バイトマシンで、32ビットCPUでは、ワード境界は4の倍数で現れ、64ビットCPUでは8の倍数で現れます。
さて、データの話にもどりましょう。最新の64ビットで説明していきたいところですが、64ビット書くのも面倒ですので、ここでは、旧式の8ビットでの説明とさせていただきます。64ビットの装置はビットが増えているだけで考え方は同じです。
先にお話しました「足し算係り」は、8ビットでのみ処理が可能とします。このため、8ビットで表せる 0~255までの数にのみ対応しています。これは入力のみではなく、出力も同じです。つまり、合計が255に収まる足し算までが限界です。
8ビットの2進数は以下のようになります。
| 十進 | 二進 |
| 0 | 00000000 |
| 1 | 00000001 |
| 2 | 00000010 |
| 3 | 00000011 |
| ・ ・ ・ |
・ ・ ・ |
| 100 | 01100100 |
| 200 | 11001000 |
| 255 | 11111111 |
| 300 | (1)00101100 |
仮に先の「足し算係りさん」に 200+100 を実行させると、平気で 44(二進では 00101100) を出力します。
演算器の出力が8ビットであるため、あふれた部分(桁あふれ)が無視されたためです。しかし、実際には、演算器は桁あふれのレジスタ(1ビットのレジスタを一般にフラグと呼び、この桁あふれを示すフラグをキャリーフラグと呼びます)を持っていて、きちんとこのレジスタに出力して注意を促します。問題はプログラムがその対応を行うかどうか(桁あふれフラグの確認処理を書いてあるか)になります。
せめて、答えのみ正しく出力させるためには、答えの領域(棚の枠)を2つ使い(16ビット)、演算器の桁あふれビットも含めて出力することです。
この話で重要な点は、8ビットのコンピュータだからといって、数値情報として0~255までしか扱えないかというとそんなことはなく、メモリの複数の枠を使うことで対応できるということです。要はプログラムの作り方次第ということです。
負の数
さて、コンピュータ上で負の数を扱うにはどうしたらいいでしょうか? 例えば「-2」という数値です。
とりあえず、演算器の動作に従って下記の演算を考えてみましょう。8ビットで答えを出す演算器での加算になります。
11111110 + 00000011 → 00000001 (桁あふれ)
桁あふれは起きていますが、8ビットの範囲では、「1」の答えがでています。足した数である「00000011」は10進数では「3」ですね。3を足して1になる数といえば -2です。つまり、「11111110」は-2です。以上です。
「さっきの話だと "11111110"は 254 になるじゃん!」となりますよね。そうです。これはどちらも正しく、"11111110"は254であり、-2でもあるのです。要はプログラムを作った人がどちらとして扱うかによるわけです。正の整数しか扱う必要のないプログラムの場合は、8ビットで 0~255を表現して扱えばいいですし、負の数を扱う必要がある場合には、演算器の動作を意識しつつ別の定義が必要になるということです。
では、負の数を扱うための定義をどうしましょうか? 演算器の加算は、下記のようなループ形態となります。ちょっと3ビットでやらせてもらいます。つまり、演算器の入出力が3ビットのレジスタであるとします。
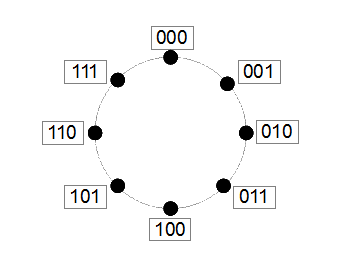
加算は、このループを右回り(時計回り)に遷移します。例えば、「001」に「2」を加算する という計算では、「001」から右回りに二つ進んで「011」となります。ところが、「数値」では、無限に大きくなっていきますが、この有限の範囲では、元に戻ってしまいます。正の整数の場合、この111→000で不連続点があるわけです。つまり、演算器のビット範囲では正しく動いていますが、計算結果としては誤った結果となる境界です。この不連続点を計算の過程で通った時、演算器は「桁あふれ」を表示するわけです。
状態の移り変わりは、負の数を考慮した場合でも同じなので、問題は、負の数を導入した時、どこを不連続点とするかになります。
最上位ビットが0から1に変わるところなんかよさそうですね。では、そうしましょう。以下の対応とします。
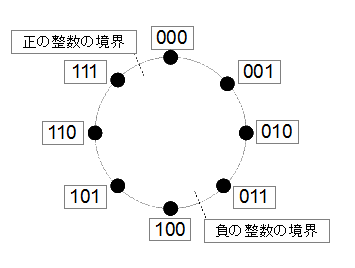
何か適当に決めた感がありますが、実際のCPUも同様の考え方になっていて、この不連続点を超えた場合にも「表示」がなされるようになっています(この不連続点を超えた場合に表示されるフラグを「オーバーフローフラグ」と呼びます)。従って、負の数を考慮した8ビットの数値の表現範囲は、-127~128になります。
一般に、負の数を考慮した2進数表現では、最上位ビットを「符号ビット」と呼んでいますが、このビットを符号に直せば負の数ができあがるわけではないのでご注意ください。あくまでも上記の論理で考えてください。
2の補数
引き算のメカニズムについて、情報処理試験などで出てくる「2の補数」も併せて説明しましょう。
先に、演算器は「加算しかできない」と書きました。加算しかできない演算器とは、上記のリング状の状態遷移で、右まわりしかできない ということです。引き算は左まわりの状態遷移になります。では、この引き算をどうやって実現するかというと、右まわりで代用するわけです。つまり、3ビットの場合、2(二進では010)を引きたい(左に移りたい)のであれば、代わりに6(二進では110)を足して(右にまわって)代用するわけです。この「2(010)」に対する「6(110)」が補数です。
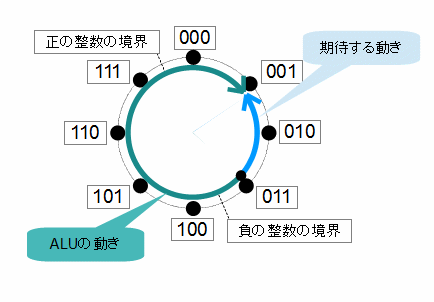
これが足し算のみに対応した演算器の引き算の方法であり、「2の補数」の意味になります。
補数の作り方ですが、元の数と補数の関係は、足し合わせると、この輪を一周することになるので、3ビットの場合は、足すことで「1000」になればよいわけです。これを簡単に作成するには、足して「111」になる値を求めて、それに「1」を加算すれば良いです。足して「111」になるようにするには、元の数のビットを反転(0を1に、1を0にする)すればよいです。その上で「1」を加算すれば補数の出来上がりです。
ちなみにCPUには「引き算命令」も用意されています。しかし、その内部では、この補数を生成して加算するという動作を実行しています。このような動作なので、引き算の場合はフラグの参照方法も変わってきます。足し算では、不連続点を超えるとフラグで注意が表示されましたが、引き算では、これらのフラグが「表示されない」ということは、本来の移動方向で不連続点を超えているわけですから、結果は誤りとなるわけです。
小数点数
これまでは、正、負も含めて整数について説明してきました。今度は小数点数です。
小数点数は表現方法がいくつもありますので、考え方のみを説明します。
10進数の整数のみを使って小数点数を表す方法を考えてみると以下のような方法があります。
-5.348 → 1:53480:-4
最初の「1」は符号を示します。0が正で、1が負です。(符号部)
次の数字は数を示す部分を小数点を度外視して5桁で示します。(仮数部)
最後の数字は、前の数に10の何乗を掛けるかを示します。(指数部)
これによって数値を示します。よろしいでしょうか?
それぞれの桁数を定義し、この約束に従って数値を表現します。もうこうなると単純な数値ではなくなり、CPUの演算器では処理不可能で、プログラムを書いて計算するしかなくなります(※ 最近のCPUでは、特定の(特定の規定に従った)小数点数は計算できるようになっているものもあります)。
このように、小数点数は、構造化されたデータ(ブロックに分かれ、それぞれに意味が規定されている)になります。単一のプログラム内のみで利用する場合は、プログラムを作る人が独自に規定すればいいですが、他のシステムとデータをやり取りする場合には、標準化された構造を使うことになります。いくつかのフォーマットがありますので、興味のある方は個別に調べてください。何れのフォーマットも、符号部、仮数部、指数部からなるのは同じで、各部分の順番やビット数が異なるのみです。コンピュータ用語では、「浮動小数点数」と呼び、表現できる大きさの違いで、「単精度」「倍精度」と呼んでいます。また、もちろんコンピュータでは、仮数部も指数部も二進で表現されることも注意してください。
さて、このような小数点数の計算(加算)はどのように行えば良いでしょうか? まず、桁を合わせる必要がありますので、指数部を見て桁合わせをするため、指数部が大きい方に合わせます。
そうした上で整数である仮数部を演算器で計算します。
ここで「この方法だと、指数部が大きく離れている数値の計算はまずくない?」と思われた方は正しいです。そうです。まずいのです。
上記の例で、仮数部が5桁で指数部が5以上離れている数値を足す場合、大きい方に桁合わせしてから計算しますので、小さい方の数は「0」になってしまうのです。整数をあえて上記の例で表現してみます。
0:12345:5 → 1234500000 0:24680:0 → 0000024680
計算対象は、上位の5桁だけですので、結果的に、ゼロを足しただけになってしまいます。
小数点数は、こういった問題があるので、会計のシステムなどでは基本的に使いません。ではどこで使うかというと、科学技術計算等で使います。「円周率の計算」などが典型です。円周率(3.14・・・)を求める式はいろいろありますが、一つ例にあげると以下です。
\[ \sum_{n=0}^\infty \frac{(-1)^n}{2n+1} = \frac{\pi}{4} \]これは「級数」という式で、nを0から増やしていきながら、シグマの右の式を足しあわせていくものです。これをnが無限大まで繰り返します。実際の計算は以下の通りです。
\[ 1-\frac{1}{3} +\frac{1}{5} -\frac{1}{7} +\frac{1}{9} -\cdots = \frac{\pi}{4} \]値をみてもらえばわかると思いますが、考え方としては、初めに大雑把な数値を求め、少しづつ補正していくイメージになります。無限大までやることはできないので、かなり大きいnまで進めることになります。これをプログラムで計算させるために、小数点数を使って行うと、初めのうちは良いのですが、nが大きくなると足す数が非常に小さくなり、ちっとも補正されなくなります。これを正しく計算するには、nが大きい方(補正値が小さい方)から計算すれば良いのです。これにより、小さい値の加算結果が大きい数に反映されます。
小数点数は他にも問題が発生する場合があります。以下の計算はいかがでしょう。
1÷3×3=?
8桁くらいの簡単な電卓でやってみると結果は、0.999999になると思います。正解はもちろん「1」です。これは電卓が有限の桁の中で計算していることが問題なのです。1÷3をやった時点で、0.333333を出し、その下の桁を無視してしまうのです。コンピュータも同様に有限の桁で計算しているため、この違いがプログラム上では問題になります。
昔、私が大学生の時、バイト先で店長が、月末になるとタイムカードと電卓で悪戦苦闘しながら時給の集計をしていたので、当時のポケットコンピュータ(電卓みたいなものでプログラミング機能があるもの)を使ってプログラムを作って使ってもらうことにしました。
その店では、バイトの給与計算に、一日のトータルの時間を20分単位で切り下げて出し、それらを月で集計(加算)し、小数点以下を切り捨ててトータル「時間」を出して時給を掛けるという方法を使ってました。これをそのままプログラムにしてしまったもんで変な結果が出ました。つまり、20分が1/3時間なので、例えば、5時間20分働いたことになった日が3日あったとしてこれらを加算して、小数点以下を切り捨てたら、15時間になってしまったのです。つまり、
5.3333+5.3333+5.3333 = 15.9999 → (小数点以下切り捨て)→ 15
ということです。もちろん本来は16時間にならなければなりません。
幸い、納品?前に気づいて、しょうがないので、一日の計算結果に少し値を足して辻褄を合せるようにしました。
(5.3333+0.01)+(5.3333+0.01)+(5.3333+0.01)=16.0299 → (小数点以下切り捨て)→ 16
実際は、補正用の値はもう少し大きな値を使ってしまったように記憶しておりますが・・・
さて、この計算処理ですが、後で考えれば20分を1として日々の計算を行うと共に、月の集計をした上で3で割ればよかったのです。
5時間20分→ 3(20分を1とした1時間分)×5+1 =16 16+16+16 = 48 48÷3 = 16
これは整数の世界でのみ計算をしていることがわかると思います。整数でのみ計算すればこのような問題は起きません。とにかく、コンピュータで小数点数を扱う場合にはご注意ください。
論理演算
先に、演算機の説明で、加算に加えて「論理演算」ができると記述しました。ここで論理演算について説明します。
論理演算では、ビットを対象とし、「1」を「真」、「0」を「偽」として扱い、二つの値に対して一つの結果を得ます。まず、「論理和」という演算では、少なくとも片方が「真」であれば結果は「真」となります。以下の通りです。
| 入力1 | 入力2 | 論理和 |
| 偽(0) | 偽(0) | 偽(0) |
| 偽(0) | 真(1) | 真(1) |
| 真(1) | 偽(0) | 真(1) |
| 真(1) | 真(1) | 真(1) |
論理和は、英語では、「OR」と言い、「A OR B」 という形で表現し、また日本語では、「A 若しくは B」と言います。すなわち、A 若しくは B が真であれば、真になる ということになります。
次に「論理積」という演算があり、これは、両方が「真」の場合のみ、結果が「真」になります。
| 入力1 | 入力2 | 論理積 |
| 偽(0) | 偽(0) | 偽(0) |
| 偽(0) | 真(1) | 偽(0) |
| 真(1) | 偽(0) | 偽(0) |
| 真(1) | 真(1) | 真(1) |
論理積は、英語では、「AND」と言い、「A AND B」 という形で表現し、また日本語では、「A かつ B」と言います。すなわち、A かつ B が真であれば、真になる ということになります。
ALUでは、これを多数の桁で同じ桁のビットに対して行います。以下に8ビットの例を示します。ここでは、両方の結果とも示しています。
| 入力1 | 10111001 |
| 入力2 | 10011110 |
| 論理和(OR) | 10111111 |
| 論理積(AND) | 10011000 |
論理和、論理積がどのようなものか理解いただいたところで、コンピュータでは、これをどのように利用するかというお話です。まず、論理和から見てみましょう。下の例を見てください。
| 入力1 | 10111001 |
| 入力2 | 00001111 |
| 論理和(OR) | 10111111 |
答えを言ってしまうと、論理和は、ビットをセットするのに使えるのです。上記の「入力1」は元のデータで、「入力2」は、元のデータである入力1のビットを操作するためのものと考えてください。入力2は、上位4ビットが「0」、下位4ビットが「1」になっています。これをORすることで、元のデータ(入力1)の下位4ビットを無条件に(強制的に)「1」にセットできていることがわかります。
次に論理積です。上記と同じ値でやってみると以下の通りです。
| 入力1 | 10111001 |
| 入力2 | 00001111 |
| 論理積(AND) | 00001001 |
論理積の場合は、「ビットのクリア(強制的に「0」にする)」という意味と、「ビットの取り出し」という意味で利用できます。上の例では、元データの入力1に対し、作用させる入力2は、上位4ビットを「0」で行うことで、上位4ビットを「クリア」しています。一方、下位4ビットは「1」にすることで、入力1の下位4ビットを「抽出」できています。
このように論理演算では、データを「ビット列」として捉えた上で、このビットを操作するために使うことができます。これを利用して数値処理とすることもありますが、後述(「データ再考」)する「数値」以外のデータでの処理に利用することが多いです。一つ、私が大学時代に作成したスケジュール管理のプログラムの例をお話ししましょう。あ、この時のバイトは先の時給計算のお話とは別のバイト先でのお話しです。
そのバイト先の会社では、大勢のオペレータの中から特定の時間帯で稼働できる人を検索する必要がありました。まず、スケジュールデータは、1日の営業時間8時間を30分で区切り、この30分間が稼働可能である場合は「1」とし、1日の一人のデータを、16ビットで表すことにしました。ある日の3人分のデータは以下のようになります。
| Aさん | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bさん | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Cさん | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
ここで、朝から3時間、動ける人を探すために、各人のデータと検索用のデータ:1111110000000000のANDを取ります。その結果が検索用のデータと同じになったら、その人は、その時間帯で稼働可能ということになります。
| Aさん | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 検索データ | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ANDの結果 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
これは、ANDによる「ビットの取出し」を利用していることになります。
あと、このお話は、「データの表現方法」という意味でもご理解ください。何がなんでも二進数ではなく、ビット情報の特性を利用すれば、様々な利用方法がある ということです。事実、この「時間帯」をビットで示す方法は、データ量の削減と検索スピードのメリットがあります。ちなみに、このプログラムは CPM-86 というOS上で動かしました。当時の遅いコンピュータでは、データ量の削減とスピードの向上は非常に重要なポイントだったのです。このCPM-86ですが、今見ようとすると博物館に行くしかないでしょうね・・・。
論理演算として、論理和(OR)、論理積(AND)について説明しました。論理演算としては、あと一つ、「排他的論理和(XOR)」というものがあります。以下の通りで、ビットが違っていると真になります。
| 入力1 | 入力2 | XOR |
| 偽(0) | 偽(0) | 偽(0) |
| 偽(0) | 真(1) | 真(1) |
| 真(1) | 偽(0) | 真(1) |
| 真(1) | 真(1) | 偽(0) |
このXORの使い方としては、「特定ビットを反転させる」があります。下位4ビットを反転させるには以下のようにします。
| 入力1 | 10111001 |
| 入力2 | 00001111 |
| 排他的論理和(XOR) | 10110110 |
ALUの論理演算は以上です。あと、一つのレジスタでビット処理を行うものがあります。反転(NOT)とシフト/ローテイトです。反転は良いでしょう。シフトはビットを1桁ずらします。シフトによってあふれたビットはフラグに現れます。ローテイトは、あふれたビットを空いたところに補います。
| 入力1 | 10111001 |
| 反転(NOT) | 01000110 |
| 入力1 | 10111001 |
| 左シフト | 01110010 |
| 入力1 | 10111001 |
| 左ローテイト | 01110011 |
シフトは演算として使う場合もあります。十進で考えていただくと、左に一桁ずらすことは、10倍することと同じです。このため、二進数では、左に一桁ずらすことは2倍することと同じになります。CPUには掛け算命令もあるのですが、この掛け算命令は、一般に処理時間がかかります。このため、単純に2倍とか4倍する処理の場合は、このシフトを使う方が短時間で完了します。
これでALUの処理が全て出そろいました。さて、ここでコンピュータの構成全体を思い返していただきたいのですが、新しいビットが生まれるのはこのALU上だけで、あとは、同じ情報を転送しているだけなのです。しかもその生まれ方は、上記の演算やビット操作の結果だけです。例えば、人間であれば「適当な数、言ってみて?」という問いに容易に対応できますが、コンピュータは無理です。どんな優秀なプログラマでも、そもそもそのALUの機能が上記の通りなので無理なのです。この「適当な数」がプログラム的に必要であれば、私なら現在の時刻の秒数とかを使って擬似的に出しますが、これは「適当な数」を言ったわけではないですね。最近、AI(人工知能)がホットだったり議論されたりしてますが、所詮ALUですからね・・・。まあ、受け売りしかできないけど、その量たるや大量である人をコンピュータで模すのをAIと言っているのならわかりますが、「知能」というのは違うと思います。皆さんはいかがお考えでしょうか?
最後にデータの表記についてお話ししておきます。コンピュータ内のデータはビットとして存在するため、「0」「1」となることに変わりはないのですが、本書のような資料であったり、後述のプログラム作成のための言語内では、「0」「1」を並べて記述するのは認識が困難だったり、間違えたりする場合があるので、もう少しわかりやすい表記が指向されます。もちろん、数値としては十進で表記すればよいのですが、桁が著しく変わるので、使いにくい場合もあります。そこで、16進数が定義されて使われることが多くなります。ビット情報では1バイト、つまり8桁(8ビット)のデータが基本となりますが、4ビットでは16通りとなり、16進数の1桁に対応でき、すなわち、16進数の2桁が1バイトに対応しますので適切です。ただ、16進数の一桁は、数値を表すために我々が使っている「数字」は0~9の十通りしかありませんので、16進数の表記には足りません。このため、アルファベットを使って補います。以下のようになります。
| 二進数 | 16進数 | 十進数 |
| 00000000 | 00 | 0 |
| 00000001 | 01 | 1 |
| 00000010 | 02 | 2 |
| ・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
| 00001001 | 09 | 9 |
| 00001010 | 0A | 10 |
| 00001011 | 0B | 11 |
| ・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
| 00001111 | 0F | 15 |
| 00010000 | 10 | 16 |
| 00010001 | 11 | 17 |
| ・ ・ ・ |
・ ・ ・ |
・ ・ ・ |
| 11111111 | FF | 255 |
ここで、例えばプログラムを作成する時の表記で「10」と記述すると、何進数で記述したのかわかりません。そこで、16進数の場合は、頭に「0x」を付けるのが一般的なルールとなっています。二進数の場合は「0b」を付けます。10進数の場合は「無し」です。
プログラム
「プログラム」について、掘り下げていきます。まず、「プログラム」についてここまで学んだことを整理しましょう。プログラムとは以下のようなものでした。
- メモリ中に、処理する順番で、個々の命令として格納されている
- 命令はCPUが実行できるもの
- プログラムカウンタが指す場所から取り出して実行される
命令は、メモリに格納されているので、ビット情報です。つまり、「0」「1」の羅列です。このため、「プログラムを作成する」とは、このビット情報でCPUが解釈できる命令を記述していくことになります。このようなビット情報形式のCPUの命令を「機械語」と呼びます。しかし、このような機械語でプログラムを作成するのはかなり面倒です。そこで、より、人が見て分かりやすい表現に変えて記述します。これをアセンブリ言語と呼びます。例えば、「演算器で加算を実行する」が機械語で「00010010」だとすると、これをアセンブリ言語では「ADD」と表現します。どちらが分かりやすいかは一目両全です。しかし、コンピュータのメモリに格納されるのも、CPUが解釈するのも「00010010」の方ですので、コンピュータ内では、どこにも「ADD」は出てきません。あくまでも、人が記述するのに便利だから「ADD」を定義しただけです。単純に机上でアセンブリ言語を使って記述するためだけに使います(ここの机上はほんとの机上です。足し算係さんの机じゃないですよ)。アセンブリ言語でプログラムを記述して、出来上がったら、機械語に変換してコンピュータ内にセットします。この「変換」を人手でやることを「ハンドアセンブル」と呼びます。昔はハンドアセンブルをする人もいましたが、今は「アセンプラ」という「道具」を使って行います。
この「道具」は、・・・「プログラム」です。機械語に変換するためのプログラムを使ってコンピュータにやらせるのです。この「機械語に変換するためのプログラム」と元々の目的のプログラムを混同しないでください。もう、なんなら「ハンドアセンブル」しかない ぐらいの理解でもいいです。
先の例でプログラムカウンタを強制的に減少させることで繰り返し処理を実現していました。実際、このような処理はプログラム中には多数出てきます。これは「プログラムカウンタをXX減らす」で実現するわけですが、このXXを数えるのは面倒です。このため、アセンブリ言語で書く時は
Lab01: 命令 命令 命令 … GOTO Lab01
などとします。「GOTO Lab01」にくるとプログラムカウンタを減らすことでLab01:の位置まで戻るようにします。
アセンブラでは、Lab01:に戻るには、幾つプログラムカウンタを減らせばいいかの計算もやってくれます。ハンドアセンブルでは、自分で数えて記述しなければなりません。
サブルーチン
プログラムカウンタの値を強制的に変更することで、プログラムの流れを変更することができたわけですが、これの別の方法について説明します。
プログラムの中で、同じ計算処理が多数出てくる場合があります。例えば、数値の階乗の計算が随所に出てくるプログラムがあったとします。階乗について少し説明します。階乗とは、ある値について、1づつ減らしながら掛け合わせて結果を求めるもので、「nの階乗」は、n!と記述し、結果の計算は、「n×(n-1)×(n-2)・・・×1」とするものです。例えば、4の階乗(4!)なら、4×3×2×1 で、「24」になります。プログラムの話に戻ります。ここまでの知識では、以下のようなプログラムになります。
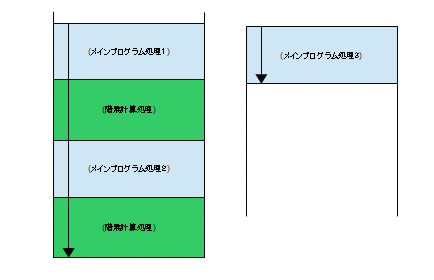
これを、「サブルーチン」を使うことで、プログラムを小さくすることが可能になります。
まず、全体のプログラム(メインプログラム)が配置されるメモリの領域以外の場所に階乗の計算処理のプログラム(サブルーチン)を記述します。この階乗プログラムは、メモリのあるアドレス(X)の値を取り込み、階乗計算し、別のアドレス(Y)に格納するという処理を実行します。メインプログラムは、階乗の計算が必要になった時点で、Xアドレスにその値を書き込み、階乗計算に移行(階乗計算のサブルーチンにジャンプ)し、サブルーチンの処理が終わると、メインプログラムに戻り、メインプログラムでは、Yアドレスから結果を取り出して次の処理を実行するという流れを実現できればいいです。
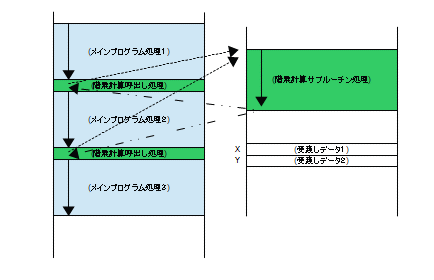
しかし、この動作は、より具体的に考察するといろいろと疑問が出てきます。メインプログラムからサブルーチンへの移行(ジャンプ)は、サブルーチンを置いてあるアドレスでプログラムカウンタを更新すればいいですが、問題は、階乗プログラムからメインのプログラムへの戻りです。ここで階乗プログラムの最後に、メインプログラムの次のアドレスへのジャンプ(プログラムカウンタのセット)を書いてしまうと、メインプログラムで、次に階乗が必要になったときにこのプログラムが使えなくなってしまいます。この問題を解決するために、メインプログラムで階乗プログラムにジャンプする前に、現在のプログラムカウンタの値を「プログラムカウンタの保存場所」(メモリ)に保持しておきます。そして階乗プログラムから戻る場合には、その保存場所に保持されている値でプログラムカウンタを書き換えます。これにより、メインプログラムのどの場所から階乗プログラムに移っても、階乗計算の後に、メインプログラムの続きの場所に戻ることができるようになります。ここまで考慮できて初めてサブルーチンという技術が利用できます。具体的に示したのが下の図になります。
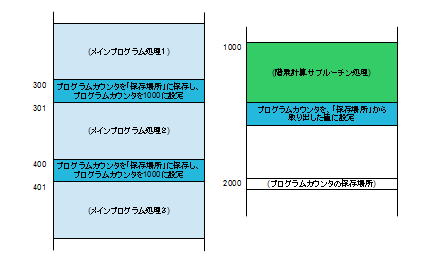
メインプログラムで階乗の計算が必要になった時点で、階乗のサブルーチンに飛びます。この処理が#300に書いてある通り、現在のプログラムカウンタを保存場所に保存して、階乗ルーチンの配置アドレスである「3000」をプログラムカウンタにセットする処理で、これはCPUの1命令で行われます。このため、命令を取り出すと次のアドレスを指すプログラムカウンタでは、保存される値は、「301」になります。サブルーチンに移行して処理が行われ、その最後にある、「プログラムカウンタを保存場所から取り出した値に設定」する処理では、先ほど保存した「301」でプログラムカウンタを更新するので、処理はメインプログラムに戻ることになります。さらに、#400でサブルーチンに移行した場合は、保存される値は「401」になり、サブルーチンからの復帰の場所も#401になります。
これでよさそうですが、実は、さらに考察が必要な点があります。問題は上記の「保存場所」になります。上記では、保存場所として単一の場所(#2000)として示しましたが、実際は違うのです。これについて解説していきます。
上記の方法(単一の場所に保存する)を取った場合に問題となる一番簡単な例は、サブルーチンの中から、別のサブルーチンを呼ぶ場合です。サブルーチンは便利なので、サブルーチンの呼び出しは一回だけなどと限定すべきではないのです。メインからサブに行き、別のサブに行ってしまうと、例のプログラムカウンタの保存場所はどうなってしまいますか?「保存場所」が単一の場所であれば、次のジャンプで上書きされ、その前の戻り場所情報が消失してしまいます。
そこで、この「退避場所」を以下のように実現します。
- 退避場所はメモリ中とする。
- 退避場所のメモリ中のアドレスを保持するレジスタを用意する。
- 退避場所への格納は、そのレジスタが示すアドレスに格納した後にレジスタの値を増加させることで行う。
- 退避場所からの取出しは、レジスタの値を減少させた後に情報を取り出すことで行う。
この方法によれば、退避場所への格納を何回繰り返しても、前の情報は残ります。さらに、退避場所からの取出しは、一番最後(最近)に格納した値が取り出されることになり、取出しを繰り返すと順番に取出されてくることになります。
この機能はCPUに設けられており、退避場所のメモリの領域を「スタック領域」(あるいは単にスタック)と呼び、このスタック領域の次の場所を示すレジスタを「スタックポインタ」と呼びます。「スタックに格納する」とは、スタックに格納することとスタックポインタの更新を含む処理になります。この動作を以下に図示します(スタックポインタは図示していません)。
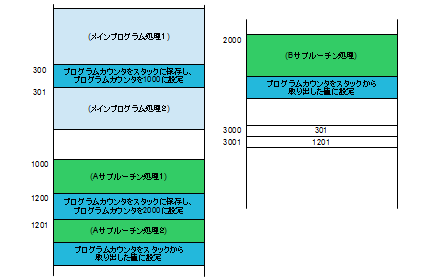
#300のAサブルーチンへのジャンプでは、スタックポインタの値は「3000」になっているため、#3000には、ここでのプログラムカウンタの値である「301」が保存され、その後、スタックポインタの値が「3001」に増加されます。Aサブルーチン内でBサブルーチンへのジャンプをすると#3001にBサブルーチンからAに戻るためのプログラムカウンタの値である「1201」が保存されます。Bサブルーチンからの戻りでは、この「1201」がプログラムカウンタに格納され、同時にスタックポインタの値が「3000」に更新されます。このため、Aサブルーチンからの戻りでは、#3000に格納されている「301」でプログラムカウンタが更新されるため、メインプログラム処理2に戻ることができるわけです。さて、このサブルーチンに移行するための「プログラムカウンタをスタックに保存し、プログラムカウンタのをXXXXに設定する」という長い命令ですが、これを「CALL命令」と呼びます。一方、サブルーチンから戻るために「プログラムカウンタをスタックから取り出した値に設定する」命令を、「RETURN命令」と呼びます。両命令とも、スタックポインタの更新処理を含むスタック処理も行います。
すみませんが、サブルーチンの話がまだ続きます。
メインプログラムでは、レジスタやメモリの領域を使って処理を行っているわけですが、サブルーチンがそのレジスタやメモリの場所を使ってしまうと値が書き変わってしまいますので、これは避けなければなりません。
このため、サブルーチン側では、その処理の最初に、CPU内のレジスタの値を保存する処理を行います。この保存先としてスタックを利用します。つまり、少なくとも自分が利用するレジスタの値をスタックに保存し、処理が終わり、RETURNで戻る前にレジスタに戻しておきます。こうすることで、メインプログラムは処理を正しく継続できます。このスタックへの保存処理は、プログラムで明示的に記述します。このスタックに格納する処理を「PUSH」、取出す処理を「POP」と呼びます。もちろん、PUSH、POPには、スタックポインタの更新処理も含みます。
サブルーチンが、その処理をレジスタのみで実行できれば、この対応だけで問題ありませんが、多くのデータを使う等でメモリも利用しなければならない場合は、どのようにメインプログラムの利用領域を保護するかが問題となります。正確には、メインプログラムというより、呼出し元のプログラムの領域の保護ということになります。
ここで少し展開から外れて考察します。
サブルーチンの例として、階乗計算を取り上げました。また、サブルーチンの中から別のサブルーチンを呼出す(ジャンプする)ことがあることも話しました。この階乗計算のサブルーチンで別のサブルーチンを呼出すことを考えてみましょう。
階乗の計算処理を考えてみると、Xの階乗を求めるには、X×(X-1)! を計算すればいいですね。となると、X-1の階乗が必要なわけで、階乗計算をしてくれるサブルーチンは・・・それって俺!? となります。つまり、自分自身を呼出して計算を依頼するわけです。これを「再帰」と呼びます。「自分自身を呼出すって何?」って感じで、ちょっとこんがらがってきましたか? 若しくは、「再帰っておもしろそう!どんなプログラムになるの!」って感じでわくわくしている方もいるかもしれません。すみませんが、ここでは、サブルーチンにおける各種処理を理解していただくことを目的にしているので、ここまでにしておきます。「プログラミング」の章あたりで触れるかもしれません。
サブルーチンの利用形態を考えていくと、再帰によって、サブルーチンの処理の途中で自身が呼出される可能性も考慮しなければならなくなります。となるとプログラムの専用のメモリの領域を定義する方法もデータの保護としては不十分ということになります。
そうなりますと、やはりスタックを使うのが適切です。つまりデータの保存場所としてスタックを利用します。CALL命令では、CPUがプログラムカウンタの保存を行ったわけですが、プログラム内で、PUSH/POP命令を使って必要なデータを保存します。
これで「サブルーチン」に関する技術の説明は終わりです。お疲れ様でした。長々説明してきましたが、ポイントは以下です。
- 同じ処理はサブルーチンとしてまとめられる
- サブルーチンへの移行はプログラムカウンタの更新で行う
- サブルーチンではスタックを多用して動作の完全性を実現する
一般にメモリの利用形態は以下のようになります。
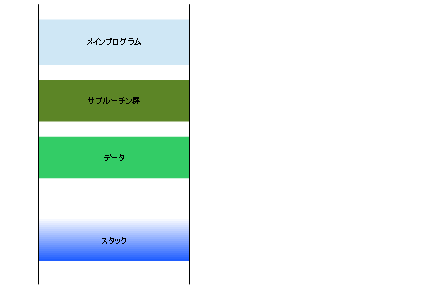
ここでスタックは、アドレスの上位から下位へと使っていくのが一般的です。つまり、PUSHでは、値を格納してスタックポインタを減少させるのです。先の説明では分かりやすくするために逆で説明しましたが、実際のCPUの動きはこちらの方です。
補助記憶装置
コンピュータは、CPU、メモリ、I/Oという基本構成があれば動きます。しかし、このメモリ、電源を切ると中身が消失してしまう(揮発性と言います)のです。メモリ中には大事なプログラムがあります。プログラムがなければCPUは動けません。電源投入直後のCPUはどうすれば良いでしょうか?
これを解消するには、メモリの一部に、電源を切っても消えない記憶領域を設ければ良いのです。このようなメモリをROM(Read Only Memory)と呼びます。電源が投入されると、CPUは、このROMの部分から命令を取出して実行を開始します。具体的には、電源投入直後のCPUのプログラムカウンタの値(概ね「0」)がこのROMの部分を差しています。しかし、このROMを巨大にしてしまうと汎用的に使える領域が減ってしまいますし、いろいろな処理に対応できなくなってしまいます。そこで、補助記憶装置を設けます。この補助記憶は電源を切っても情報が消えないもので実現します。現在は、一般的にはハードディスクです。ROMには、この補助記憶装置からプログラムを読み込んで実行を開始するプログラムを書いておきます。このようなプログラムをブートローダと呼びます。ブートローダは補助記憶装置の特定の場所からプログラムを取出してメモリに配置し、そのプログラムを実行します。では、このプログラムはどのようなプログラムでしょうか? このプログラムが特定の目的のプログラム(例えばワープロ用)であると、このコンピュータはワープロ専用機になってしまい、汎用性がなくなってしまいます。このプログラムは「他のプログラムの実行を支援するプログラム」です。いわゆる「オペレーティングシステム」です。これ以降は「オペレーティングシステム」の項で説明します。
補助記憶装置は、電源を切ると内容が消えてしまうメモリを「補助する」ものですので、「プログラム」の他に「データ」も配置されます。
さて、ここで、「どうして、メモリを、補助記憶装置と同様の技術で、電源が切れても内容が消えないように構成できないのか」と疑問に思われないでしょうか。この理由は、速度とコストにあります。大量のデータを更新可能で保持し、なおかつ電源消失時にも保持した値を消えないように構成したものは、非常に高価になります。安く作れなくもないのですが、安く作ったものは、今度は速度が遅くなります。この「安く作ったもの」の代表例がハードディスクになるのですが、あるサイトの情報では、メモリが1に対して、ハードディスクは10万倍の時間がかかるそうです。これでは比較になりません。一方、高価な投資をして消えないメモリを作っても、所詮はCPUのアドレスバスのサイズなので、コンピュータで利用する全てのプログラムやデータを保存しておくには、別の記憶装置が必要になります。やはり、メモリは比較的安価で高速な揮発性メモリで構成し、補助記憶として、大量の情報を保持できる不揮発性の記憶装置を利用し、都度補助記憶装置から必要なプログラムやデータを取り出して記憶した上でメモリ中で作業を進めるのが適切ということになります。
割り込み
ここで割り込みという機能について説明します。
CPUは電子部品で、多数のピンで他の部品と電気的につながっています。この中に割り込み用のピンがあります。このピンに信号が入ってくると、CPUは現在の内部状態(プログラムカウンタやレジスタ)をスタックに保存して、割り込み用に設定されているアドレスにジャンプします。ここに割り込み用のプログラムを記載しておき、割り込みを契機としてプログラムを実行することができます。このプログラムが終了するとCPUはスタックから情報を取出し、元の状態に復帰させます。
割り込みは外部からの指示により実行されるサブルーチンと言えます。
割り込みがどのように使われるかを説明します。
例えば、一定時間(1秒間)毎に処理をするプログラムを考えます。「ストップウォッチ」などが適切でしょう。この場合、今までの知識の範囲で「ストップウォッチプログラム」を作るには、各命令が実行するのにかかる時間を調べて計算する必要があります。昔のCPUの命令は、各命令毎に処理にかかる時間が決まっていましたので、ある程度は時間を把握できましたが、今のコンピュータでは、これは難しくなっています。なぜかというと、CPUが高速になりすぎて、メモリの速度が追い付いていないため、メモリからの取り出しや書き込みに待ち時間が発生し、かつ、メモリの種類によって、この待ち時間が変わります。また、メモリの状態によっても時間は変わります。まあ、昔の遅いCPUも最新のCPUも、時間を把握することは困難であるわけです。
このため、CPUの外部にタイマ用の部品を用意し、この部品から得られる定期的な間隔の信号をCPUの割り込み用のピンに接続して一定時間毎に割り込みがかかるようにします。ここでは、0.1秒毎に、このタイマ部品からの信号が出されるものとします。このタイマ割込みを利用して動作する「ストップウォッチプログラム」は以下のようになります。
最初に、割り込みが発生した時用の準備をします。割り込みが発生した時に動くプログラムとしては、Aレジスタの値を増加させるプログラムにします。一方、メインのプログラムでは、スタートするとAレジスタの値をゼロにし、その後はAレジスタの値を秒に換算して(10倍して)表示する処理を、ストップされるまで延々繰り返す処理になります。そうするとメインのプログラムでは、一切、Aレジスタの値を変更していないのですが、割り込み用のプログラムが更新するので、結果的に表示が変化することになります。
このようにメインプログラムの実行とは無関係に発生する状態を検知し、プログラムで利用する技術が割り込みです。
割り込み用の端子はCPUに用意されている数本しかありません。しかし、現実には、多くの割り込みを処理したくなります。例えば、皆さんがお使いのコンピュータでは、入力装置全てが割り込みを発生させます。キーが押された、マウスが操作された等です。このため、割り込みコントローラという部品が設けられております。多数の装置からの割り込みをそれぞれ受け、まとめてCPUに送ります。このような構成では、割り込みを処理するプログラムでは、最初に割り込みコントローラから、今発生した割り込みの詳細を取り出し、それに対応したプログラムを実行するように構成します。
ここでちょっと展開から外れますが、折角、時間の話をしたので、少し考察しておきましょう。
「割り込みが0.1秒毎に発生する」となると、割り込み処理ばっかりやることにならないか という心配はないでしょうか。そこで計算してみましょう。CPUは周期的な信号を発生する部品の音頭取りで処理を実行します。この周期的な信号を「クロック」と呼び、クロックの1周期が「cycle」です。CPUの性能を示す指標として、「XXGHz」といっているあれです。最近の一般的なCPUは1~3GHzといったところでしょう。割り込み処理用のプログラムが消費する時間を1000cycleとしましょう。1000cycleあれば、そこそこの処理ができます。CPUのクロックが1GHzの場合は、1秒間は、1,000,000,000cycleです。割り込みが1秒間に10回発生し、それぞれに1000cycle使うとすると、1秒間に10,000cycleです。これは全体の100,000分の1です。この「100,000分の1」を、一か月(30日)で換算してみると「26秒」という答えがでます(一月の100,000分の1が26秒)。一月に26秒間だけ話しかけてくるだけの人を、こいつが邪魔するから仕事にならないなどとは言えませんよね。つまり、この程度ではほとんど問題になりません。コンピュータがどれくらい早く処理をするかがおわかりいただけたのではないかと思います。
高級言語
コンピュータの正体を理解してもらうために、ここまでは、プログラムを構成する命令はビット情報であり、これを機械語と呼び、プログラムを作成することはつまり機械語を順番に並べることだと説明してきました。もちろん事実なのですが、現在、この機械語を使ってプログラムを作成している人はまずいないでしょう。まあ、それは当然ですが、アセンブリ言語を使っている人も極めて少ないでしょう。では、どうやってプログラムを作成するかといえば、「高級言語」と呼ばれるもので作成されています。
例えば、高級言語で足し算プログラムを書くと以下のようになります。
LABEL1 : INPUT A INPUT B C=A+B OUTPUT C GOTO LABEL1
「INPUT」はキーボードから入力される値を変数に格納する命令です。「変数」とは、一時的に値を格納する枠です。最初のINPUTは「A」という変数に格納します。次に同様に「B」という変数に格納して、次の「C=A+B」で、これらの値を足して変数「C」に格納します(一般の言語では、このような書き方が使われます。イメージとしては、C←A+B になります)。そして、「OUTPUT」は変数の値を画面に出力する命令です。これで足し算を実行し、また最初に戻ります。
もう、レジスタとかメモリの何番目のアドレスなど全く出てきません。
このように高級言語では、かなり人間に近い(人間にとって便利な)表現になっていると思います。「高級」といっているのは、別に価値が高いというわけではありません。人間に近いものを「高」、機械に近いものを「低」と言っています。このため、機械語やアセンブリ言語は「低級言語」と呼びます。しかし、実際にはCPUが実行するので、最終的には機械語に直してメモリに配置し実行される必要があります。このため、高級言語で記述されたプログラムは「コンパイル」という処理を経て機械語に変換されます。
アセンブリ言語では、アセンブリ言語で記述された命令を1対1で機械語に変換します。このため、CPU内のレジスタや演算器の動作を理解した上でプログラムを作成する必要がありました。しかし、高級言語のコンパイルでは、ひとつの命令を多数の機械語命令に変換することも行なってくれるので、より人間に近いイメージでの処理記述を可能にします。
例えば、上記の「INPUT A」などは、本当は、キーボードからの入力を受けるために、キーボードが接続されているI/Oのアドレスを把握しなければなりませんし、入力されるまでの待つ処理も必要です。また、「A」は実際にはCPU内のレジスタやメモリの一部を使って値の保持をするわけですから、そこに保持する処理になおさなければなりません。これらのもろもろの面倒な処理を「コンパイラ」が変換してくれるので、プログラムを作る人は、楽ができるわけです。もちろん、この「コンパイラ」も人が作ったわけですが・・・・
高級言語でプログラムを記述したものを「ソースコード」と呼びます。最終的に、機械語での記述となった本当のプログラムを「バイナリコード」と呼びます。ソースコードをコンパイラにかけて変換(コンパイル)することでバイナリコードが得られます。
高級言語でソースコードを作ることは、人に近い世界でのプログラミングを可能にすることに加え、他にもメリットがあります。
CPUはいろいろな会社で作られており、また、同じシリーズでも機能が追加されていたり等で様々です。機械語はCPUの命令そのものなので、CPUが変わって使うレジスタが変わったりすると、都度バイナリコードを書き変える必要があります。しかし、高級言語のソースコードは維持できる場合が多いです。つまり、そのCPUの違いへの対応をコンパイラが行ってくれるのです。一般に、コンパイラはCPUと共にCPUの製造会社から提供されます。
コンパイラを使ってバイナリコードを得るタイプの他に、「インタプリタ」方式と呼ばれる高級言語があります。インタプリタでは、ソースコードを「プログラム」に渡し、一命令ずつ実行してもらいます。イメージ的には、この「プログラム」は、サブルーチンの塊のようなもので、ソースコードが実行の順番を指定しているようなものです。このため、同じ処理内容のプログラムを、コンパイラ方式の高級言語で作成して実行した場合と、インタプリンタ方式の高級言語で作成して実行させた場合では、コンパイラ方式のプログラムの方が高速になる傾向があります。しかし、例えば業務処理系のプログラム(例えば会計システム等)では、ほとんどの時間はユーザの入力待ちになりますので、あまり高速でも意味がなかったりします。どの高級言語を利用するかは、また別の面でのメリット/デメリットを考慮して選択することになります。ただ、映像処理のためのプログラムでは、時間のほとんどがCPUの処理時間になりますので、コンパイル方式の高級言語で作成されることが多いです。コンパイル方式の言語の代表例は、「C言語」ですが、このC言語は、低級言語的な使い方も可能になっているもので、映像処理に限らず、高速な処理が必要なプログラムは、概ねこのC言語で作成されることが多いです。
オペレーティングシステム
コンピュータは電源が投入されるとCPUが動作を開始します。CPUがやることは、プログラムカウンタが示すアドレスから命令を取出し、実行するを繰り返すことでした。ところが、メモリは、一般的には、電源が入れられた時には空です。プログラムがないとCPUは意図した動作を実行できません。そこで、電源が切られても内容が消えないメモリ(ROM)を使って最初に実行するプログラムを保持します。つまり、電源が投入されたCPUは、プログラムカウンタの値が、このROMのアドレスを差しており、ここからプログラムを実行開始します。では、ここに記述されているプログラムは具体的に何を行うのでしょうか。ここに四則演算プログラムがあると、コンピュータは単なる電卓になってしまいます。やはり、いろいろなプログラムを必要に応じて実行できるようにするのが適切でしょう。このため、「いろいろなプログラムを必要に応じて実行できる状態を作る」プログラムがあるべきです。
オペレーティングシステム(OS)にはいろいろな側面がありますが、この「いろいろなプログラムを必要に応じて実行できる状態を作る」のも一つの役割です。従って、最初に実行されるプログラムは、このOSであるべきです。しかし、ROMにOSを入れてしまうと、違うOSやOSの機能変更に対応できなくなります。そこで、ROM上には、補助記憶装置(例えばハードディスク)の特定の場所からプログラムを取出してメモリに配置し、その先頭アドレスから実行を開始するプログラムを置くことでOSの変更に対応でき、汎用性(いろいろなことに対応できる)が高まります。
OSのプログラムが実行されると、「いろいろなプログラムを必要に応じて実行できる状態」が作られます。この状態は、皆さんが目にしている、画面上にいろいろなプログラムのアイコンが表示されている状態です。ここから、実際に各プログラムを実行していきます。このコンテンツをご覧になっているということは、Webブラウザ(IE、Firefox等)を動かしているわけで、これがプログラムの実行の結果であるわけです。このような特定の目的のために実行するプログラムをユーザプログラムと呼びます。ユーザプログラムは、OSに添付されているものや自分で入手してインストールしたもの、自分で作成したものといろいろあります。これに対して、「いろいろなプログラムを必要に応じて実行できる状態」を作っているOSのプログラムを、ユーザプログラムと一線を画し、「カーネル」と呼びます。つまり、例えばWindowsを購入すると、IE、メモ帳といった付属のユーザプログラムに加え、この「カーネル」が入っています。OSとしての本体は、このカーネルにあります。以降、「OS」といった場合はカーネルと思ってください。このカーネルについてこれから説明していきますが、これはOSの種類(windows、android、iOS、linux等)によらず、全てに共通のお話です。
システムコール
プログラムを作成する時、サブルーチンは便利なものでした。特に他人が作成したサブルーチンを入手して利用させてもらえばプログラムの作成が省力化できます。OSには多くのサブルーチンが用意されておりこれが利用できます。OSのサブルーチンを呼出すことを「システムコール」と呼んでいます。例えば、皆さんがお使いのブラウザも内部でシステムコールを多用しています。私はブラウザのプログラムの中身を見たわけではありません。「それじゃぁ私の使っているブラウザはシステムコールに頼ることなく、開発者が自分で全部作っているかもしれないじゃん」 と言われるかもしれませんが、間違いなく使っているのです。これは、システムコールはプログラム作成の省力化を図るだけでなく、システムを保護するためにも使われているためです。つまり、コンピュータ内の資源、特に入出力装置に関しては、システムコールを使わないと利用できないようになっていたりするのです。このような構造にすることで、間違った使い方をユーザプログラムにさせないようにしているのです。このあたりのメカニズムについては、今までお話しておりませんので、おいおい説明していきます。
とにかく、OSはシステムコールを通じてユーザプログラムに各種機能を提供する これがOSの第一の機能です。
OSが用意しているシステムコールは多種多様なものがあり、これらはサブルーチンとして分かれているわけですが、これらの機能の全てを予めメモリ中に配置してしまうと、ユーザが実行するプログラムによっては、使用されないものもありますので、無駄になってしまいます。これを、ユーザのプログラムが実行された時に、若しくは本当にその処理が必要になった時に配置できれば、メモリ利用の観点では有効になります。これを実現する方法がダイナミック・リンク・ライブラリというものです。プログラムの作成においては、単純に必要なシステムコールを実行する処理を記述します。しかし、これがダイナミック・リンク・ライブラリによる実現であれば、コンパイルしても、その部分は実際のプログラムにはならず、OSにXXXXという名のライブラリを実行を依頼する という処理に変換されます。そして、このプログラムが実行された時にOSがこのライブラリを探して(ディスク中のファイルから探す)実行します。
マルチプログラミング
皆さんがお使いのコンピュータですが、複数のプログラムを同時に実行させていませんか。例えば、ブラウザでWebを見ながら、メディアプレイヤーで音楽を再生する といったことです。このような動作をこれまでの知識で実現しようとする(プログラミングしようとする)と大変なことになります。このような形態はCPUの助け(機能)とそれを利用したOSの機能によって実現されます。複数のプログラムを同時に実行する形態を「マルチプログラミング(マルチタスク)」と呼び、OSの重要な機能になります。
CPUがプログラムを実行しているイメージは、マルチプログラミングでも今まで見てきた動作と同じです。人が机について仕事をしているイメージです。異なる点は、短い時間でその人の仕事が切り替わる点です。どちらかと言うと、「人」が入れ替わると考えていただいた方がわかりやすいでしょう。つまり、Aさんがブラウザ用のプログラムを実行しており、Bさんは音楽再生のプログラムを実行しています。非常に短い時間で見た時は、机で仕事をしているのはAさんかBさんですが、順番に切り替わって仕事をしているので同時に行っているように見えるのです。Aさんが仕事をしている時にBさんはどうなっているかというと、「凍りついて」いるイメージです。Bさんに順番が回ってきたら急に溶けて動き出すのです。机やメモリの状態も凍りつく前の状態であれば、何事もなかったように仕事を続けれらます。もっと言えば、凍りついていた事実すらなかったように見えます。では、このAさんとBさんを切替える作業は誰がやるかと言うと、これがOSの役割なのです。
しかし、Aさんが実行している時、OSはどうしているかというと、やっぱり凍りついているのです。ここで登場するのが割り込みです。Aさんが実行している時、規定の時間が来ると割り込みが発生します。そうするとCPUはAさんの状態をスタックに退避し(この時点でAさんは凍りつきます)、割り込み用のプログラムに移行します。この「割り込み用のプログラム」はOSなのです。起きだしたOSは、管理簿としてメモリ中に保存してある情報を参照し、Aさんの持ち時間が一旦終了したことを認識し、次のBさん用の保存されている状態をCPUに戻します。この時点でBさんの動作は再開し、OSは凍りつくわけです。
このように割り込みによって必ずOSが介入しつつ処理が進めれられていくわけです。ただ、AさんにしてもBさんにしてもそれぞれの目線でみれば、まるで自分がCPUを占有して動いているように見えるでしょう。このようにすれば、これまで説明した普通のプログラムとして作成されたプログラムであってもマルチプログラミング環境で動くことができるわけです。
ここで用語の定義です。プログラムはメモリ中の命令群です。実行されているプログラムをプロセスと呼びます。先のAさん、Bさんはプロセスです。OSもプロセスになります。もう一つ用語の紹介です。この「短い時間でプロセスを切り替える」ことを「タイムシェアリング」と呼びます。
さて、CPUの状態は割り込み機能によって退避され、前に凍りついた時から再開できたわけですが、メモリはどうでしょう。メモリの状態も凍りつく前の状態が維持されなければなりません。他のプロセスが誤って自分のメモリ領域を書き換えてしまうことなどあってはならないのです。このために棚を複数用意して、それぞれの棚を個々のプロセスに割り当てます。実際には、棚は連続しているので、棚の番号を、アドレスの上位に持ってくることで識別します。以下のようなイメージです。例によって本来二進数であるアドレスをあえて十進のイメージで書いておりますので、一万の位がプロセスの識別用です。
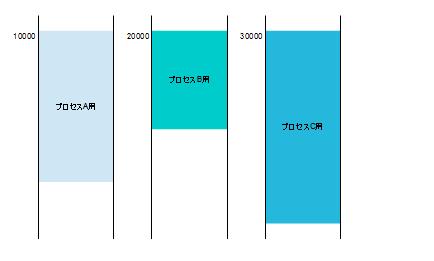
CPUは、プログラムを取り出す場合やデータを取り出す場合にアドレスを指定しますが、プロセスが指定するアドレス(プロセスのプログラムが操作するプログラムカウンタやデータのポインタ)は、この上位を除く下位のみで行います。しかし、実際のメモリのアクセスには、この上位を加えた形でアクセスするのです。この上位部分もCPU内のレジスタによって指定されるのですが、このレジスタは一般のプロセス(ユーザ)は書き換えることができないのです。どういうことかというと、CPUには特権命令と分類される命令があり、CPU内のあるフラグがセットされていないと、この特権命令が実行できないのです。OSの実行中は、このフラグがセットされています。OSはユーザプロセスに処理を渡す時に、このフラグをクリアしてから渡します。このフラグがセットされて特権命令を実行できる状態を特権モード(カーネルモード)と呼びます。
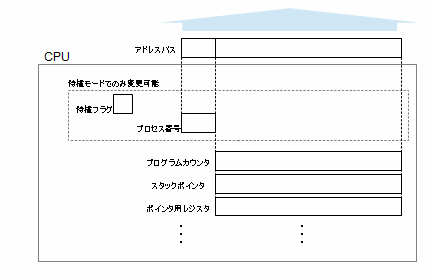
このような構成により、プロセスは、どう頑張っても自身に割り当てられたメモリ以外の領域にアクセスすることができなくなっているので、他のプロセスの領域を侵食することがないのです。また、プロセスの切り替え時に退避したり、更新するレジスタには、このプロセス番号のレジスタも含まれます。
待ち状態
コンピュータでは多くの入出力が発生します。例えばワープロソフトでは、キー入力によって文字を羅列していきますが、どんなに人間が早くタイプしても、コンピュータの速度にはかなわず、キー入力を待つ時間が多数発生します。最初の方で説明しました動作では、キー入力があるかをチェックする処理を繰り返すことで入力待ちの状態を作っていたわけですが、これはCPUにとっては無駄な時間であるわけです。特にマルチプログラミングでは、そんな時間は別のプロセスに開放してやるべきです。先に、入出力関連はシステムコールによりOSの機能を呼出すとお話しました。つまり、この時点でOSの処理に移っているわけです。OSは、そのプロセスが入出力を要求したことを記録した上で、他のプロセスに処理を渡してしまいます。要求したプロセスもOSも寝てしまいます(凍りついてしまう)が、入出力が発生すると割り込みが発生します。これを契機として先のプロセスを再開させることができ、また、入出力待ちの時間を別のプロセスに割り当てることができるわけです。もし全てのプロセスが待ち状態に入るとCPUを一時停止させ、消費電力を下げたり、温度を下げることもできます。
ここで文献に出てくるプロセスの状態遷移について見ておきましょう。
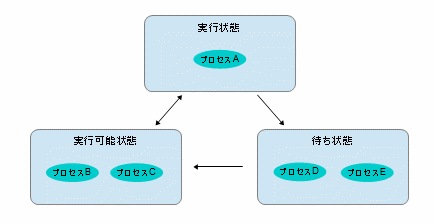
プロセスは、三つの状態が定義されています。CPUに割り当てられ、実際に動いている状態が「実行状態」です。もちろん、この状態にあるプロセスは、一つだけです。先に短い時間で切り替えられるのは、「実行可能状態」にあるプロセスが対象です。つまり、この図の状態で、次の切り替え時間が経過すると、プロセスB、Cのどちらかが「実行状態」に移り、プロセスAは「実行可能状態」に遷移することになります。プロセスD、Eが置かれている「待ち状態」が先の入出力装置の完了を待っている状態です。例えば、プロセスDが待っている入出力の完了が起きると、プロセスDは「実行可能状態」に移行します。また、この図の状態でプロセスAが入出力のシステムコールを発行すると、プロセスAは「待ち状態」に移行し、空いた「実行状態」には、プロセスB、Cのどちらかがアサインされます。
この、各種文献で出てくるプロセスの状態を示す「待ち状態」というのは、あくまでも入出力等の完了を待っている状態のプロセスを示す用語であることをご理解ください。タイムシェアリングで、自分の順番を待っているプロセスは「待ち状態」ではなく、「実行可能状態」です。
マルチスレッド
マルチプログラミングは、同一コンピュータ上で複数のプロセスを実行する技術です。この時、各プロセスは独立しています。先に例を上げた通り、ブラウザとメディアプレイヤー等が例で、これらは別のプログラムで、別に連携して処理をしているわけではありません。単一のコンピュータの中で複数のプロセスを動かし、待ち時間を利用してコンピュータを効率的に利用することができます。
しかし、単一の目的を持ったプログラム(例えばワープロソフト)の中で、入出力の待ち時間の中で別の処理を実行したい場合があります。今までのお話の中では、入出力が発生した時点で、プロセスの実行権限は奪われてしまいます。これを回避し、一つのプロセスの中で、複数の実行実体(スレッド)を作成することができるようにしたものがマルチスレッドです。もちろん、プログラムの作成はスレッドを意識して行う必要があり、また、スレッドに対応した言語を使う必要があります。
プロセスとスレッドの大きな違いは、メモリの利用にあります。プロセスは元々、独立性を作り出すものでしたのでメモリは別空間で、他のプロセスのメモリは触ることができませんでした。スレッドはメモリが共用なので、簡単にスレッド間でデータのやりとりができます。
もしプロセス間でデータのやり取りが必要な場合は、プロセス間通信というOSの機能を使う必要があります。イメージ的には、ネットワークを介して通信する感じになります。ほとんど使う必要はないと思いますので、詳細は割愛します。
仮想メモリ
各プロセスが実行している時のメモリの状態は、以下のようになっていると説明してきました。引き続き、十進表示での説明にさせていただきます。プロセスの番号による識別は、千の位で行うものとします。点線のラインは、100毎に枠を分けています。プロセスAはプログラム、データ、スタックで600分の枠(バイトマシンでは600バイト)を利用しますので、このような割り当てです。ちょっと小さすぎるので現実的ではありませんが、あくまでも考え方を示すための想定です。

ここで、すごい技術が登場しました。それが「仮想メモリ」です。仮想メモリを利用すると、メモリの利用は以下のようになります。各プロセスは上の図と同じです。
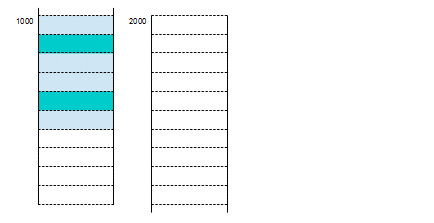
まず、驚くべき点の一つ目は、配置されている量の少なさです。600バイト必要なプロセスAが400バイトしか配置されおらず、同様にプロセスBに至っては200バイトだけです。さらに二つ目として、プロセスA用の利用メモリの間にプロセスBのメモリが配置されてます。これが仮想メモリを利用した場合のメモリの利用状態になります。何やら、今まで説明してきた内容が根底から覆されそうですが、ご心配には及びません。増加していくプログラムカウンタも、増減するスタックポインタも変わりません。プロセスは連続したアドレスの空間に自身のプログラムが配置されているものとしてアクセスする(命令を順番に取出していく)のですが、実際のメモリ上では、飛び飛びの場所に配置されているのです。プロセスが指定するアドレスをリニアアドレスと呼び、これは連続であり、プログラムカウンタ等に保持されている値です。しかし、アドレスバスに出ていくアドレスは結果的に飛び飛びになっています。じゃあ、こんなことをしているのは誰の仕業かと言えばCPUしかありません。CPU内で変換されているのです。このため、CPUには以下のような機構が設けられます。プログラムカウンタのみ示します。
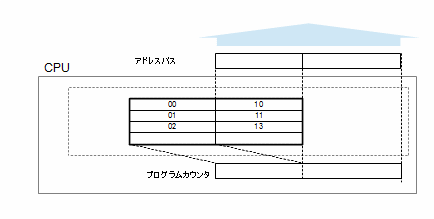
前のメモリの図に従い、こちらも十進で説明を続けます。これは、先の図のプロセスAが実行中のCPU内のアドレス変換機構を示しています。このアドレス変換機構に表のように示されているのが変換テーブルです。この変換テーブルは特殊なメモリであるCAM(Content Addressable Memory)というもので構成されています。通常のメモリは枠を示すアドレスで特定し、その枠内の情報をデータとして取り出しますが、CAMでは、枠内に保存されている値で枠を特定し、その枠に関連したデータを取り出します。上図を見てください。プログラムカウンタの上位部分で、左側の枠を検索し、合致したエントリの右側の枠の値をアドレスバスの上位に出しています。では具体的にいきましょう。プロセスAが#0000からプログラムをスタートします。プログラムカウンタは「0000」から開始されますが、この変換テーブルにより、実際のメモリは#1000から命令を取り出します。動作が進み、プログラムカウンタが、「0099」の時は、まだ最初のエントリに合致するので、#1099からの取り出しになりますが、プログラムカウンタが1増加して「0100」になると、次のエントリに合致し、アドレスバスに出ていくアドレスは「1200」になり、いきなり100分スキップすることになります。これが実際のメモリ中に連続して配置されていなくても良い理由です。
次に、プログラムカウンタが「0299」から「0300」になり、リニアアドレスとして「0300」になった時です。03用のエントリがアドレス変換機構にありません。しかし、メモリ中には4番目のエリアが配置されています。変換テーブル内にエントリが存在しない場合、変換テーブルをCPUが作成します。この変換テーブルの元となる情報はメモリ中に記述されており、この変換テーブルの場所(アドレス)を保持するレジスタがCPU内にあります。CPUはこのアドレスから、変換テーブルの情報を取り出し、CPU内のアドレス変換機構に新しいエントリを形成し、処理を継続します。この動作は、CPUの機能として動きます。つまり、ここではOSは動きません。しかし、このメモリ中の変換テーブルを作っておくのはOSの役目です。また、CPUのレジスタに、このテーブルの場所を設定するのもOSの役目になります。
さて、次です。今度は、プログラムカウンタが、「0399」から「0400」になった場合です。CPUはアドレス変換機構にエントリが無いので、メモリに探しに行きますが、メモリ内の変換テーブルに「未」の印を発見します。これは、未だメモリ中に配置していないことを示します。この状況になると、CPUは、割り込みを発生させ、OSに処理を依頼します。これを受けたOSは、プロセスの必要な部分をメモリに配置し、変換テーブルを作成し、役目を終えます。CPUはもう一度、プログラムカウンタによるアクセスから開始し、アドレス変換機構のサーチを行い、存在しないので、メモリから取り出しを行い、今度は取り出しに成功し、アドレス変換機構のエントリを形成し、処理を継続できるわけです。
さらに、メモリが一杯になっている状態(大量のプロセスが起動し、OSが全てのメモリを割り当てた)で、新しいプロセスの起動が必要になると、既に使われているメモリのエリアを補助記憶装置に退避させてエリアを開け、新しいプロセスに割り当てるのです。この動作を「スワップアウト」と呼びます。動作が別プロセスに移行し、そのプロセスが、このスワップアウトされてたエリアを使うことになると、別のエリアをスワップアウトし、そこに補助記憶から取り出して配置します。これを「スワップイン」と呼びます。スワップアウトするエリアは、なるべく使用される可能性が少ないものを選ぶと効果的ですが、この選択方法はコンピュータの動作の効率に影響しますので、OS、正確にはOSを作った人の腕の見せ所です。
いかがでしょうか。仮想メモリの技術を使うことで、以下の効果が得られます。
- プロセスは、最小限のメモリで開始でき、必要に応じてメモリを利用できるため、メモリの効率的利用が可能になる
- プログラムの作成時に広大なメモリ空間の利用を前提とすることができる
一方で、この機能は、スワップアウトが適切に行われないと、スワップイン、スワップアウトが繰り返し行われ、非効率な動作となる危険性もはらんでいます。これを「スラッシング」と呼びます。仮想メモリの機能は、今やほとんどのOSに組み込まれていますが、仮想メモリ機能があるからといって、少ないメモリしか実装しないとか、大量のアプリを同時に起動しておくとかはやめるのが適切です。
さて、延々、仮想メモリのお話しに、十進のアドレスを使ってきてしまったので、ここらで、本来の二進でのお話しとしましょう。32ビットのCPUのお話しです。プロセスが利用するプログラムカウンタは32ビットです。ですからとんでもなく大きいプログラム(4Gバイトまで)が作成できます。一方、実装できるメモリも、アドレスバスが32ビットなので、4Gバイトまでです。仮想メモリの技術がなければプロセスが使える領域と実装メモリの最大値が同じなのはあり得ないのですが、皆さんはもう理解できていると思います。さて、十進での説明で、100バイト単位で区切っていましたが、これはアドレスの下位12ビットとなっているのが一般的です。このため、4096バイト(4Kバイト)単位での割り当てとなります。さらにこの単位を「ページ」と呼びます。
つまり、OSは、1ページ分である4kバイトのメモリを割り当てのみでプロセスをスタートさせることができます。さらに、あるプロセスがシステムコールを要求して配置したルーチンを、他のプロセスが同様のシステムコールを発行した場合に、同じものを利用することも可能です。つまり、先に説明しました「ダイナミックライブラリ」については、そのプログラム部分を複数のプロセスで共有させることも可能になります。
データ再考
ここまでの説明では、データとして「数値」を扱ってきました。もちろん、「計算機」として利用されるコンピュータでは、数値を扱うことが主目的なのですが、現在、皆さんのコンピュータの利用目的はかなり違うと思います。Webを見たり、動画を見たり、音楽を聞いたり、といった感じでしょう。むしろ、「計算」なんてしたことがない というのが現実でしょう。そうなると必然的に、扱う「データ」も違ったものになっています。
ここでは、多様化しているデータについて、その考え方を説明します。
全てのデータを考察する場合、重要なのは、コンピュータ内では、全て「0」「1」で表現する必要がある、つまり、ビット情報に変換する必要があるということです。これを「コード化(encode)」といいます。コード化されたデータを元に戻すことを「復号化(decode)」といいます。
文字データ
何といっても、一番身近なデータは、この文字データです。Webを見るのも、メールを見るのも、この「文字」が主役です。
さて、この「文字」をどのようにしてビット情報にするか ですが、これは単純に対応関係を決めてしまえばいいでしょう。例えば、「A」という文字ならば「01000001」としましょう といった具合です。しかし、一文字表すのに何ビット使うかという問題があります。
コンピュータの初期は米国で発展を遂げました。米国で使用される「文字」は、「数字」「アルファベット」「記号」程度で、種類としては比較的少ないので、8ビット(256通り)=1バイトもあれば十分です。むしろ多すぎて、実際は7ビットで表現して対応付けました。この対応をASCIIコード(若しくはASNコード)と呼びます。1ビットは使用せず(「0」で固定)、1文字を1バイトでコード化しておりました。
しかし、現在は、全世界でコンピュータが利用されています。日本を考えても、どれだけの文字がありますか。「ひらがな」「カタカナ」「漢字」全部合わせると何通りでしょうか。一方、お隣の韓国ではハングル文字がありますし、中東ではアラビア文字もあります。これらを統一的に扱う必要があります。まあ、各国でそれぞれ決めればいいんじゃないの という考えもあるでしょうが、いやいややっぱり統一的に決めましょうよという考え方もあります。そいういったいろいろな考え方で、いろいろな文字コード体系ができてしまっているのが実情なのです。
日本語に限定して、この文字コードの代表的なものを挙げてみますと以下のようになります。
| コード名 | 概要 | 備考 |
| Shift-JIS | WindowsOSで利用されていた日本語用の文字コード | |
| EUC-JP | UNIXで利用されていた日本語用の文字コード | UNIXはOSです |
| UTF-X | 国際標準として規定された文字コード。Xには数字が入り、具体的なコードになります。 | UTF:Unicode Transformation Format |
現在では、WindowsもUNIX(LINUX)も国際標準を受けてUTFを使うようになっていますので、今後はUTFを利用する方向で問題ないです。
UTFの種類としてよく目にするのはUTF-8とUTF-16です。新しめのWindowsの内部で利用されているのはUTF-16ですが、一般的に多く利用されているのはUTF-8になります。ここではこのUTF-8について説明します。
UTF-8は「マルチバイト文字」という形式で、文字によってコード化された結果の長さが違います。上記のASCIIコードはそのままの形で利用され、これは1バイトでコード化されます。次に2バイトにコード化されるグループがあり、続いて3バイトにコード化されるグループがあり、この3バイトのグループに、日本語のひらがな、カタカナ、漢字が含まれます。最後に4バイトにコード化されるグループがあり、これで全部です。つまり、日本語の文字データでは、ASCIIと一般の日本語で記載されることが多いと思いますので、1文字が1バイトになるものと3バイトになるものが混在する形で文章全体がコード化されることになります。
UTF-8でコード化されたテキストの任意の1バイトを取り出した時に混同することがないように、3バイト文字には1バイト文字のコードが含まれないように規定されています。このため、1バイト文字では、00~FF(16進数表記です)までの全てのパターンを使用せず、00~7Fまでを使って対応を取ります。これにより、80~FFまでを使って2バイト以上の文字のコード化を行うことになります。同様に2バイト文字で使用したコードの2バイトのパターンを使用することなく3バイト文字のコード化を行います。このようにマルチバイト文字では、1バイト文字でも00~FFまでの256パターンを全部使えるわけではないことに注意してください。
文字の一生
では、ここで、「文字」がコンピュータ上で生まれて使われていく様子を見てみましょう。
とりあえず、例の足し算プログラムで、極めて基本的な部分を理解していきます。ここでは日本語は登場しません。つまり、取り扱う文字コードは、ASCIIの1バイト文字です。
足し算プログラムでは、入出力装置から「値」を受け取って、加算結果である「値」を表示するわけですが、この部分を明確にしましよう。
「値」の入力に入出力装置であるキーボードが使用されますが、キーボードのキーを押すと、そのキーに対応したコードがキーボードからコンピュータ本体に送られます。このコードは、ASCIIとして扱いやすいように、ASCIIコードが利用されます。しかし、数字を入力しやすいように構成されているテンキーでは、別のコードが使用されています。足し算プログラムではテンキーを使うことにします。テンキーで、各キーが押された場合の送信されるコードは以下の通りです。このコードをキーコードと呼びます。
| テンキーの数字 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| キーコード | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 |
加算する数が「123」の場合、テンキーを「1」「2」「3」と順に押します。するとキーコードとして、「97」「98」「99」が送られます。プログラムでは、入力者が入れやすいように、画面上に入力された数字を表示するように作るのが一般的でしょう。画面上に表示されている文字は、点の集まりである画像です。いわゆる「フォント」というものです。「1」用のフォントがコンピュータ内部に用意されており、これを画面上に点の集まりとして表示するわけです。このフォントはASCIIコードに関連づいています。
| 文字(数字) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| ASCIIコード | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 |
フォントを表示するため、キーコードを一旦ASCIIコードにします。キーコードから「48」を引くとASCIIコードになります。これを利用してフォントを参照し、画面に表示します。
さて、これでとりあえず、入力はASCIIコードで表現された3つの文字となります。計算対象は「値」なので、これを値にしなければなりません。まず、一文字づつ値にしましょう。ASCIIコードから「48」を引くと「値」になります。
次に全体の「値」を得ましょう。一桁目はそのまま、二桁目は10を掛けて、三桁目は100を掛けて足し合わせることで「値」になります。
計算結果を表示する場合も、「値」を「文字」にしてフォントとして表示することになります。
このキー入力の受付や画面表示の処理はOS等がやってくれるのでプログラムを作成する人はここまでプログラム化する必要はありませんが、キー入力や画面表示は、基本的には「文字」であることを認識していただきたいと思います。
では、今度は日本語文字の旅を見ましょう。
コンピュータの世界で文字の旅といえばメールを考えるのが適当だと思いますのでメールを例にしましょう。
元々、皆さんがお使いのメール(インターネットメール)はUNIXが発祥です。厳密にはインターネット自体がUNIXというOSのためのものでした。UNIXは米国で生まれたので、メールもASCIIコードでやりとりしていたわけです。そして日本も仲間に入れてくださいとなります。日本語でメールを送りたくなったので、「JIS」というコード化方式を作りました。先に挙げたShift-JISというコード体系は、このJISを元に作られたもので、互いの変換が容易に行えるようにしております(変換する際にずらす(Shiftする)だけで良い)。
さて、旅の始まりです。皆さんがWindows上で文章を作成する際にはShift-JISが基本的に利用されます。日本語の入力には、「日本語入力フロントエンドプロセッサ」が動きます。皆さんが、漢字変換等を行うあれです。今では、この用語は使われなくなってきていて、Windowsでは、「IME:インプットメソッドエディタ」と呼んでいます。これで漢字を入力すると、内部的にShift-JISのコードとなります。これを受けてメールソフトでは、JISに変換して送信します。このJISでネットワーク上を転送され、相手のメールソフトが正しくJISとして認識し、日本語のフォントで画面表示されれば旅は終わりです。しかし、転送の途中で、極めて旧式のメールサーバがあったとしましょう。メールはメールサーバを経由して転送されていきます。このメールサーバが、文字はASCIIのみとして、文字の1ビットを無視(クリア)して転送してしまうとどうでしょう。到着した先で正しく認識しても意味のない文字の羅列となってしまいます。このような現象を「文字化け」と呼びます。文字化けは、システム間での文字コードの認識誤りや、システムの誤動作によって発生することがあります。誤動作はともかく、認識誤りについては、早く全世界のシステムが同一のコードを扱うようになってほしいものですが、時間がかかるでしょうね。
画像データ
画像をコード化する場合、基本的には、点の集まりとしてコード化するわけで、これはフォントの場合と同じです。単純なフォントとの違いは、各点に色の情報が必要なことでしょう。
コード化では、「点」をどのくらい細かく切るかということが重要です。細かく切れば画像はきれいになりますが、情報量は多くなります。
次は、その「点」の色の情報をどうするかです。点として1ビット使えば白黒になります。1バイトになれば256通りの色を対応付けられます。要は点毎の情報を増やすことで色の表現が細かくなり、美しい画像が表現できることになります。現在、使用頻度の高いものは、3バイトで表現するものです。RBGという光の三原色の量をそれぞれ1バイトで表現します。これはフルカラーと呼んでいます。この上にはトゥルーカラーという4バイト使用するものもありますが、色の数は同じで、透明度(下が透けて見える)を付加したものとなっています。
では、このフルカラーで計算してみます。少し前に一般的であったPCの画面は1024×768の点の集まりで、点の数は 786,432 になります。それぞれが1バイトの色情報を持つので、この画面いっぱいに表現された画像のサイズは、786,432バイト(768kバイト)になります。これは結構大きいサイズで、保存にも大きな領域を必要としますし、インターネット(Webサイト)上で使うことを考えると、ネットワークを介した転送等で不利です。ちなみに、この点の情報をそのままコード化する方法を「ビットマップ」と呼びます。
そこで考え出されたのが圧縮技術です。つまり、画像の品質の低下を最小限に抑え、全体のサイズを小さくするものです。例えばFAXでこの圧縮方法を考えてみましょう。FAXは白黒で、普通の書類であれば、ほぼ白の点でしょう。黒を「1」、白を「0」で表現すると、ほとんど「0」になります。FAXでは横並びの点を順番に表しますが、白何個、黒何個、白何個・・・と表していくと、ほとんどの文書で全体の情報の大きさが小さくなります。しかし、横並びで、白と黒が1つずつ交互に現れるものを送ろうとすると、逆に全体のサイズが大きくなってしまいます。でも、そんな書類はまずありませんので、効果的な圧縮が可能です(実際のFAXではもう少し違う形態で圧縮しています)。
圧縮方法の基本的な考え方は、元データに現れる出現パターンで、頻繁に表れるパターンを短いコードに変換し、頻度の少ないパターンを長いコードに変換することで全体の量を少なくするものです。このため、頻度が少ないとされていたパターンが大量に現れると、圧縮効果がなくなるどころか、逆に大きくなってしまう場合もあります。
ここまでの説明の「圧縮」では、元のデータを圧縮して、転送や保存を行い、表示や印刷する際には元のデータに戻すことを想定して説明してきましたし、皆さんもそのようにイメージされていると思います。しかし、現在、実際に使われている「圧縮」では元の情報に完全には戻さない(戻せない)圧縮方式もあるのです。「そんなのダメじゃん!」と思われるかもしれませんが、上記の説明で「品質の低下を最小限に抑える」というのがポイントです。画像では、厳密に再現せずに大幅にカットしてしまっても人の目にはわかりにくい部分もあり、このポイントに着目して高い圧縮率(圧縮するとより小さくなる)を実現するわけです。実際に使われているJPEGという画像圧縮の方式は、なめらかに色が変化する部分を荒くすることで情報を削減します。このため、写真などの圧縮に適しています。圧縮には「可逆圧縮」と「非可逆圧縮」という分類があり、文字通り、「可逆圧縮」は完全に元に戻せる圧縮で、「非可逆圧縮」は完全には戻せない圧縮です。もちろん、JPEGは非可逆圧縮に分類されます。画像における可逆圧縮の例としては、GIFと呼ばれる方式があります。この方式は、ベタ塗りの多い漫画などに適したものです。本サイトの図は、このGIFで圧縮しています。図がきたないのはGIFのせいでなく、元からです。
音データ
効果音だったり、音楽だったりの音のコード化です。
音は、時間で変化する空気の振動です。横軸を時間にし、縦軸をレベル(音圧)で表現すると下のように波になります。
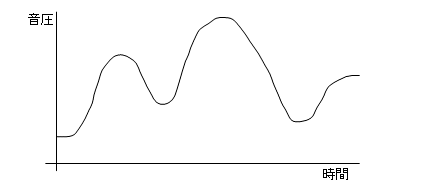
これをマイクで拾うと同じ波形で縦軸が電圧となって現れます。これを非常に短い時間で電圧の高さを値にしてコード化するのが音声データのコード化方法です。こうしてコード化した音を音に戻す(デコード)には、もちろん、同じ時間間隔でコードを電圧にして出力すればいいです。
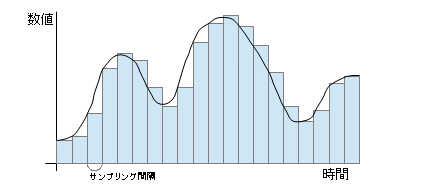
この短い時間間隔で電圧を数値化することをサンプリングと呼び、時間間隔をサンプリング間隔と呼びます。このサンプリング間隔をどの程度にするかによって、データの品質が決まります。まあ、画像における点の数と同じですね。あと、その数値化をどの程度の大きさにするかも品質に影響します。つまり、画像における色の種類ですね。
CDでは、1秒間を44100に切り、2バイト(16ビット)で数値化します。サンプリング間隔は1秒間の回数ということでHz(周期/秒)で表します(サンプリング周期)ので、44.1kHzと示されます。このサンプリング間隔を決定した理由ですが、音の波形をこのようにコード化した場合、どうしても高い周波数、つまり、短い時間で激しく変化する部分は消えてしまいます。この方法では具体的には、サンプリング間隔の半分の周波数より高い音は消えてしまうのです。つまり、CDでは22kHzですね。オーディオの世界では人が聞き取れる周波数は20kHzまでとしておりましたので、この値が選択されました。
しかし、最近では、「もっと聞こえるぞ!」ということで、より高い周波数まで保存できるようにサンプリングを96kHzや128kHzとし、また数値化も24ビットとかにして保存したものを「ハイレゾリューションオーディオ(ハイレゾ)」として出されてきています。
逆に電話等では、そんなに美しく聞かせる必要もないので、3.4kHzを上限として決めています。これを4kHzとして、サンプリング周波数は8kHzとし、また、数値化も1バイトで十分としています。
このように音声信号をサンプリング間隔で数値化するコード化方法をPCM(pulse code modulation:パルス符号変調)と呼びます。これが画像におけるビットマップ相当です。ということは、当然、圧縮の話も出てきます。代表的なものは、MP3でしょう。MP3は非可逆圧縮です。
動画データ
動画は、「動く絵」と「音声」で構成されます。音声については、先の「音データ」のコーデックを使います。以降では「動画」は動く絵のみを示すことにします。さて、この動画ですが、絵を動かすには、静止画を短い時間で切り替えていけば動画になります。切り替える時間は、動画の品質によりますが、一般的には、秒間で30枚です(これを「30fps」と言います。fpsはFramePerSecondです)。そうなると、先に画像データのところでお話しした1024×768の画像が768kバイトのサイズなので、1秒間の動画は、23Mバイト程度となり、一般的な動画では、とんでもないサイズになってしまいます。そこで、動画については、圧縮が基本です。つまり、撮影したカメラの上では、例外もありますが、コンピュータ上では、「圧縮された形式」が基本です。
その圧縮方法ですが、静止画+差分という形で行います。「静止画」は、先の画像の圧縮技術が利用できます。そして「差分」はその中で変化した部分のみの情報を持たせることで圧縮を実現します。これが動画における圧縮の方法になります。
高速化技術
基本的なコンピュータ技術は全てご説明いたしました。ここでは、処理の高速化のために付加的に利用される技術について簡単に説明します。
キャッシュ
先に記憶機構の速度についてお話ししました。ここでまとめてみると以下の通りになります。
| 速度 | コスト(ビット当たりの単価) | |
| レジスタ(CPU) | 高速 | 高 |
| メモリ | 中(CPUの10~100倍の時間) | 中 |
| ハードディスク | 低(メモリの10万倍の時間) | 低 |
技術の進歩によって、CPUの速度は高速化されているのですが、メモリの速度は追いついていないのが実情です。CPUの実行には、都度、メモリからの命令取出しが必要ですので、結局はメモリの速度に縛られてしまいます(このようなことを、「メモリがボトルネックになる」と表現します)。もちろん、メモリが高速化されれば良いのですが、現在の技術では難しいです(あくまでもコストをおさえつつ という条件の下です)。この速度差問題を解消する技術がキャッシュになります。
キャッシュは記憶機構の速度差の問題を解消するものなので、CPUとメモリ間、CPUとハードディスク間といった形で、いろいろな場所で使われます。先の問題提起に従い、まず、CPUとメモリの間での転送で考えましょう。プログラムの取出しでは、メモリから順番に命令を取り出すのが基本的な動作なので、引き続く動作では、現在取出したアドレス以降のアドレスからプログラムを取り出すケースが非常に多いです。そこで、CPUとメモリの間に、高速に動作する記憶機構(これが「キャッシュ」です)を設け、CPUが命令を解読している時や、CPU内のレジスタのみで命令が実行している時などの、アドレスバス/データバスが使われていない時間を利用してその先のアドレスからプログラムを取出し、キャッシュに格納しておきます。これにより、次の命令取出しでは、既にキャッシュ上にその命令が取り出されているので処理の高速化が実現できます。
キャッシュは有効な技術なのでCPU内部に配置されるようになってきています。このため、CPUの処理も変わってきます。これまでCPUでは、プログラムカウンタの値がアドレスバスに出て、それに対応してメモリから出力された「命令」がデータバスを介してCPU内に取り込まれる動作でしたが、CPUのメモリアクセスはキャッシュアクセスに置き換えられ、メモリアクセスはキャッシュ上にデータが存在しない場合や「先読み」のために発生するようになります。このキャッシュとメモリのやり取りは、これまで説明してきましたCPUの動作とは独立して動作していきます。
別のキャッシュの例としてはハードディスクのためのキャッシュがあります。ハードディスクから情報を取り出すと、同時にハードディスク内のキャッシュにも同じ情報が保存されます。一般的には、ハードディスク上の情報は「ファイル」として扱われますので、この「ファイル」としてのくくりでキャッシュ上に配置され、次に同一ファイルへのアクセスが発生するとキャッシュから情報を渡せるため、処理が高速化されます。
キャッシュの実現技術は複雑なため、ここでは、技術の目的のみ提示に留め、以降は詳細が必要になった方(CPUやOSを開発する方)の勉強に期待したいと思います。では、その目的です。
ヒット率の向上
必要な情報がキャッシュ上にあったことを「キャッシュにヒットした」と言います。キャッシュにヒットしなければ遅い記憶機構へのアクセスが必要になりますので、この「ヒット率」を上げることが処理速度の向上につながります。単純に考えれば、キャッシュを大きくすればよさそうですが、巨大化は、「だったらメモリを高速化しろよ」となり、本末転倒です。また、キャッシュのサーチ技術(該当エリアを探し出す)は、あまり大きくすると時間がかかるという弊害が発生します。小さいキャッシュでいかにヒット率を上げるかということになるわけです。キャッシュへの読込については、「メモリに順番にアクセスする」形態が一般的であるため、「先読み」によって、その先のエリアを読込んでおくことが、一般的には功を奏します(ただし、ジャンプが発生すると無駄になる可能性はあります)。問題は、キャッシュが一杯になった時に、どのエントリを上書きするかという点です。単純に考えれば、ほとんどつかわれていないエントリを対象にすればよいですが、この「ほとんど使われていない」を判断する印を付けることが難しいのです。このあたりがキャッシュ実現の肝になります。
同期
キャッシュは、もちろん、データとして使われるエリアについても行われます。そうなると、キャッシュ上でデータの変更が行われ、一時的でもキャッシュと、その実態である元のエリアで内容の不一致が発生します。これをどのタイミングで一致させるかという問題です。簡単なのは、速やかに元のデータを変更することですが、この度に遅いアクセスが発生することになります。ベストは、ずっとキャッシュ上で変更を繰り返し、「本当に必要になった」時点で一致させれば良いです。この本当に必要になった時点をどう判断するか これが第二の肝になります。
パイプライン
これまで見てきたCPUの処理は、命令の取出し→命令の実行→命令の取出し→命令の実行・・・を繰り返す動作でした。当然ながら、命令の実行が終わってから命令の取出しを始めるわけです。これを以下のようにするのがパイプラインです。
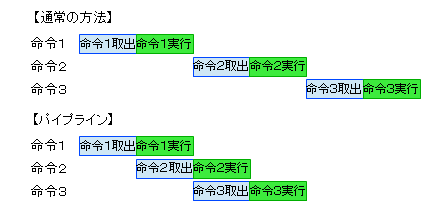
命令の実行中に次の命令の取出しを、ほんとに同時に行います。これにより、処理時間の短縮化が実現できるわけです。イメージとしては、最初に説明しました机について作業をしている人が二人いる状況です。一人は命令の取出しを専門に行うことになります。
なお、実際のCPUでは、もっと多くの処理に分割されます。つまりもっと多くの人が動いているイメージです。命令の取出し(一般に「取出し」のことを「フェッチ」Fetchと呼びますので、これを「命令フェッチ」と言います)は一人がやりますが、「命令の実行」を複数の人で分担して行うわけです。例えば下記のような分担です。これはCPUに依存します
- 命令フェッチ
- 命令解読
- 命令実行(演算処理等)
- 命令実行(メモリアクセス)
- 命令実行(レジスタへの書込み処理)
命令実行についても、このように幾つかのブロックに分けて同時実行(命令1がメモリアクセスをしている時に次の命令2が演算をしている)できるように構成するわけです。
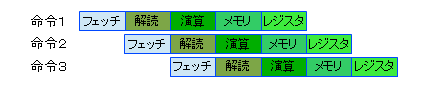
パイプラインによって処理が高速化できるのですが、このパイプラインを効果的に動作できるように、命令の内容も設定します。例えば、上記のパイプラインでは、「メモリ上のデータを加算する」という処理を行う単一の命令は使えません。演算処理は対レジスタのみとして命令を規定すれば、上記のパイプラインは構成できます。このような目的で、命令をシンプル化し、パイプラインに適したものとしたCPUを、Reduced Instruction Set Computer:RISC と呼びます。このようなRISCが登場したことで、これまでのCPUは、Complex Instruction Set Computer:CISCと呼ばれました。RISCは命令がシンプルなので、CISCでは1命令で実行できていた処理を複数の命令で実行する必要ができてたわけで、プログラムを作成する側の負担は上がるわけですが、結果的には、処理の高速化が実現できています。
マルチコア
システム全体の処理効率を上げる ということを考えれば、当然出てくる発想はCPUを増やす です。これを汎用的なCPUの内部で行ったものがマルチコアです。
マルチプログラミングでは、タイムシェアリングで、単一のCPUを使って複数のプロセスが実行していたわけですが、本当に複数のCPUを使ってこれを行う方法も使われていました。要するに机が二つあって、二人がほんとに同時に動いている状況です。ただし、これは以前の大型コンピュータ(かなり高価で巨大なもの)での話です。近年の技術進歩に伴い、小さなCPUチップの中に、複数のCPUの実体を「コア」として形成し、比較的安価に提供できるようになり、皆さんのコンピュータに実装されるようになったわけです。これがマルチコアのCPUです。
マルチコアのCPUで、どのコアを使って処理を行わせるか、つまり、プロセスへのコアの割り当てはOSの仕事になります。このあたりの詳細は知りませんが、基本的には順番に割り当てる(ラウンドロビンと言います)方式が一般的と思います。
上記を読んで、若しくは既に知識をお持ちで、ご自分のコンピュータでCPUの状態を確認した方もいるかと思います。windowsで、「タスクマネージャ」を起動し、「パフォーマンス」を参照するとCPUの使用率がリアルタイムで表示されます。その際、新しいCPUをお使いであれば、複数のCPUが表示ます。ここで、「あれ、私のCPUは4コアだと思ったのに8つも出てるよ?」となった方がいるかと思います。これは、Intel CPUの独自機能であるHyper Threading Technologyというものを利用しているためです。これは一つのコアで二つのプロセスを動作させるものです。これまでの例えで言えば一つの机に二人がついて仕事をしているイメージです。机には処理に必要なレジスタ群、プログラムカウンタ、ALU等が2セット置いてあり、その二人にアサインされております。この二人は、先のパイプライン形態で動作します。この動作により、単一のコアでも二つのコアに見せかけているわけです。
ダイレクトメモリアクセス
ここまでの説明では、コンピュータ内では何をするのもCPU任せでした。例えば画面に表示している文字や画像をスクロールすることを考えると、入力装置である棚の一つの枠が画面の1ドットに対応しているとすると、その点の情報を端から全部ずらさなければなりません。これはCPUが、棚の枠からデータを取出し、レジスタに格納し、そのレジスタのデータを別の枠に格納するという処理を画面全体にわたって順番に行う必要があるわけです。また、メモリの領域をディスクに保存する場合も、一枠ずつ取り出してはディスク装置に接続された枠に移すという処理が必要です。このような処理からCPUを解放するための技術がダイレクトメモリアクセス(DMA)です。
DMAにはDMAコントローラという構成が必要です。DMAコントローラはメモリ間での転送を実行します。DMAコントローラへの指示はCPUの仕事です。「XXXアドレスからXXXバイト分をXXXアドレス以降に転送せよ」というふうに指示します。この指示だけを行い、CPUは別の仕事に移行するわけです。もちろん、DMAコントローラもデータバス/アドレスバスを使って処理を進めますので、メモリアクセスはCPUかDMAコントローラの競合が起き、待たされることもありますが、全体の処理は効率化されます。
入出力装置には、DMAの機能を持っているものもあります。例えばディスク装置では、CPUが、「XXXアドレスからXXXバイト分をディスクに保存せよ」と指示し、ディスク装置が自身でメモリにアクセスして情報を取出します。このようにして、メモリの領域を転送する(バルク転送と呼びます)処理からCPUを解放する技術がDMAになります。